题目内容
10.下列数据中,可以算出氢气密度的是( )| A. | 氢气的摩尔质量和阿伏伽德罗常数 | B. | 氢气分子的体积和阿伏伽德罗常数 | ||
| C. | 氢气的摩尔质量和氢气的摩尔体积 | D. | 氢气分子的质量和氢气分子的体积 |
分析 密度等于质量除以体积;气体分子间隙大,分子密度不等于物体密度;固体和液体分子间隙小,分子密度等于物体密度.
解答 解:A、已知氢气的摩尔质量和阿伏伽德罗常数,可以估算氢气分子的质量,故A错误;
B、由于气体分子之间的距离比较大,所以已知氢气分子的体积和阿伏伽德罗常数,不能计算出1摩尔氢气的体积,也不知道氢气的摩尔质量,所以不能计算密度,故B错误;
C、摩尔质量除以摩尔体积等于密度,故C正确;
D、已知氢气分子的体积和氢气分子的质量,可以得到氢气分子的密度;但气体分子间隙大,故氢气分子密度不等于氢气密度,故D错误;
故选:C
点评 本题关键明确:气体分子间隙大,分子密度不等于物体密度;气体密度等于分子质量与每个分子占据的体积的比值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如图所示,两星球相距为L,质量比为mA:mB=1:9两星球半径远小于L.从星球A沿A、B连线向星球B以某一初速度发射一探测器,只考虑星球A、B对探测器的作用,下列说法正确的是( )

| A. | 探测器的速度一直减小 | |
| B. | 探测器在距星球A为$\frac{L}{4}$处加速度为零 | |
| C. | 若探测器能到达星球B,其速度可能恰好为零 | |
| D. | 若探测器能到达星球B,其所受的合力先变小后变大 |
5.“探路者”号宇宙飞船在宇宙深处飞行过程中,发现A、B两颗天体各有一颗靠近表面飞行的卫星,并测得两颗卫星的周期相等,以下判断正确的是( )
| A. | 天体A、B的密度不同 | |
| B. | 天体A、B的质量一定相等 | |
| C. | 两颗卫星的线速度一定相等 | |
| D. | 天体A、B表面的重力加速度与它们的半径成正比 |
15.某物体受到-2N•s的冲量作用,则( )
| A. | 物体初动量方向一定与这个冲量的方向相反 | |
| B. | 物体末动量一定是负值 | |
| C. | 物体动量的增量一定与规定的正方向相反 | |
| D. | 物体的动量一定减小 |
2.真空中有两个静止的点电荷,他们之间的相互作用为F,若将它们所带电荷量都增大为原来的2倍,距离减少为原来的$\frac{1}{2}$,则它们之间的相互作用力变为( )
| A. | 16F | B. | 8F | C. | 4F | D. | 2F |
20. 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )| A. | 图线1表示水平分运动的速率图线 | |
| B. | 图线2表示竖直分运动的速率图线 | |
| C. | t1时刻物体的速度方向与初速度方向夹角为45° | |
| D. | 以上说法都不对 |
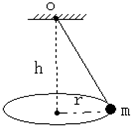 如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.
如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.