题目内容
15.如图1所示,在x0y坐标系中,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,紧靠极板的右边缘的有界匀强磁场区域由△AB0和矩形0BCD构成,其中∠0AB=60°,0D=OA.磁场方向垂直于x0y平面向里,D、A位于y轴上.位于极板左侧的粒子源沿x轴向右接连发射质量为m,、电荷量为+q、速度相同的带电粒子,现在0~3t0时间内两板间加上如图2所示的电压,已知t=0时刻进入两板间的粒子,在t0时刻射入磁场时,恰好不会从磁场边界射出磁场区域且圆心在x轴上,上述l、m、q、t0为已知量,U0=$\frac{m{l}^{2}}{q{{t}_{0}}^{2}}$,不考虑P、Q两板电压的变化对磁场的影响,也不考虑粒子的重力及粒子间的相互影响,求:(1)t=0时刻进入两板间的带电粒子射入磁场时的速度;
(2)匀强磁场的磁感应强度的大小及磁场区域的面积;
(3)t=t0时刻进入两板间的带电粒子在匀强磁场中运动的时间.
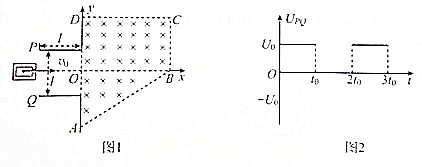
分析 (1)t=0时刻进入电场的粒子t0时刻刚好射出电场,做类似平抛运动,根据类似平抛运动的分运动公式列式求解即可;
(2)t=0时刻进入两板间的粒子恰好在t0时刻射入磁场、且恰好不会从边界HG、FG射出磁场区域;画出临界轨迹,然后结合几何关系求解出半径;最后根据洛伦兹力提供向心力列式求解出匀强磁场的磁感应强度;
(3)t0时刻进入极板的带电粒子在两个极板间做匀速直线运动,在2t0时刻沿着x方向进入磁场,进入磁场后做匀速圆周运动;画出运动轨迹,然后根据t=$\frac{θ}{2π}T$和T=$\frac{2πm}{Bq}$求解时间.
解答 解:(1)t=0时刻进入电场的粒子t0时刻刚好射出电场
带电粒子沿着x轴分速度大小为:v0=$\frac{l}{{t}_{0}}$,
y轴负方向偏移距离:y=$\frac{1}{2}•\frac{q{U}_{0}}{ml}•{{t}_{0}}^{2}=\frac{1}{2}l$
粒子离开电场沿y轴负方向分速度为vy,则有:$\frac{1}{2}l=\frac{{v}_{y}}{2}{t}_{0}$
射入磁场的速度大小$v=\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\frac{\sqrt{2}l}{{t}_{0}}$,与y轴夹角为45°;
(2)设粒子在磁场中做匀速圆周运动的半径为R1,由几何关系得:
${R}_{1}=\frac{\sqrt{2}}{2}l$,
则OA=$\frac{{R}_{1}}{tan30°}=\frac{\sqrt{6}l}{2}$,OB=$\frac{3\sqrt{2}}{2}l$,
$Bq{v}_{1}=m\frac{{{v}_{1}}^{2}}{{R}_{1}}$,
解得:$B=\frac{2m}{q{t}_{0}}$,
磁场的面积S=$(\frac{1}{2}+1)×\frac{\sqrt{6}l}{2}×\frac{3\sqrt{2}l}{2}=\frac{9\sqrt{3}{l}^{2}}{4}$
(3)t0时刻进入极板的带电粒子在两个极板间做匀速直线运动,在2t0时刻沿着x方向进入磁场,进入磁场后做匀速圆周运动,设半径为R2;
${R}_{2}=\frac{l}{2}$,
$T=\frac{2π{R}_{2}}{{v}_{0}}=π{t}_{0}$,
设AD=a,则有:
$2{R}_{1}+\frac{l}{2}=asin60°$,$a=\frac{2\sqrt{6}+\sqrt{3}}{3}t$,
因为($\frac{a}{2}-{R}_{2}$)sin60°>R2,粒子不会从PG边射出磁场,粒子在磁场中运动时间:
t=$\frac{T}{2}=\frac{π{t}_{0}}{2}$
答:(1)t=0时刻进入两板间的带电粒子射入磁场时的速度大小为$\frac{\sqrt{2}l}{{t}_{0}}$,与y轴夹角为45°;
(2)匀强磁场的磁感应强度的大小为$\frac{2m}{q{t}_{0}}$,磁场区域的面积为$\frac{9\sqrt{3}{l}^{2}}{4}$;
(3)t=t0时刻进入两板间的带电粒子在匀强磁场中运动的时间为$\frac{π{t}_{0}}{2}$.
点评 本题关键明确粒子的运动规律,然后分类似平抛运动和匀速圆周运动过程列式求解,磁场中运动注意画出临界轨迹,结合几何关系求解半径

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | 天体A、B的密度不同 | |
| B. | 天体A、B的质量一定相等 | |
| C. | 两颗卫星的线速度一定相等 | |
| D. | 天体A、B表面的重力加速度与它们的半径成正比 |
 如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )
如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )| A. | A球线速度必定等于B球的线速度 | |
| B. | A球对筒壁的压力必定大于B球对筒壁的压力 | |
| C. | A球角速度必定大于B球的角速度 | |
| D. | A球的运动周期必定大于B球的运动周期 |
 当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )
当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:($\sqrt{2}$-1) |
 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )| A. | 图线1表示水平分运动的速率图线 | |
| B. | 图线2表示竖直分运动的速率图线 | |
| C. | t1时刻物体的速度方向与初速度方向夹角为45° | |
| D. | 以上说法都不对 |
 如图为氢原子的能级图,已知可见光的光子的能量范围为1.62~3.11eV,锌板的电子逸出功为3.34eV,那么对氢原子在能级跃迁的过程中辐射或吸收光子的特征认识正确的是( )
如图为氢原子的能级图,已知可见光的光子的能量范围为1.62~3.11eV,锌板的电子逸出功为3.34eV,那么对氢原子在能级跃迁的过程中辐射或吸收光子的特征认识正确的是( )| A. | 用氢原子从高能级向基态跃迁时发射的光照射锌板,一定不能产生光电效应现象 | |
| B. | 用能量为11.0eV的自由电子轰击,可使处于基态的氢原子跃迁到激发态 | |
| C. | 处于n=2能级的氢原子能吸收任意频率的紫外线 | |
| D. | 处于n=3能级的氢原子可以吸收任意频率的紫外线,并且使氢原子电离 |
| A. | 建立“质点”和“点电荷”的概念时,利用了假设法 | |
| B. | 用电磁炉,其原理是利用了电磁感应的涡流来进行加热 | |
| C. | 开普勒对“自由落体运动”和“运动和力的关系“的研究开创了科学实验和逻辑推理相结合的重要科学研究方法 | |
| D. | 牛顿发现了万有引力定律并用实验方法测出引力常量的数值,从而使万有引力定律有了真正的实用价值 |
 如图,一质量m=2kg的物体静止在光滑水平面上,在方向为水平向右、大小为4N的恒力F的作用下开始运动,求物体经过3s:
如图,一质量m=2kg的物体静止在光滑水平面上,在方向为水平向右、大小为4N的恒力F的作用下开始运动,求物体经过3s: 一个小型应急交流发电机.内部为n=50匝边长L=20cm的正方形线圈,总电阻为r=1.0Ω.线圈在磁感应强度为B=0.1T的匀强磁场中,绕垂直于磁感线的轴匀速转动.发电机对一电阻为R=9.0Ω的电灯供电,线路中其它电阻不计,若发电机的转动角速度为ω=100rad/s时,电灯正常发光.求:
一个小型应急交流发电机.内部为n=50匝边长L=20cm的正方形线圈,总电阻为r=1.0Ω.线圈在磁感应强度为B=0.1T的匀强磁场中,绕垂直于磁感线的轴匀速转动.发电机对一电阻为R=9.0Ω的电灯供电,线路中其它电阻不计,若发电机的转动角速度为ω=100rad/s时,电灯正常发光.求: