题目内容
9. 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )| A. | 弹簧最大弹性势能为10 J | B. | 弹簧最大弹性势能为15 J | ||
| C. | 运动时间为$\frac{{\sqrt{3}}}{10}$s | D. | 落地点到桌子边缘的距离是$\sqrt{3}$m |
分析 小球离开平台做平抛运动,平抛运动在竖直方向上做自由落体运动,根据h=$\frac{1}{2}g{t}^{2}$求出小球空中运动的时间,由公式vy=gt求出小球落地时竖直方向的分速度,从而得知水平分速度.研究弹簧弹开小球的过程,由系统的机械能守恒求弹簧最大的弹性势能.
解答 解:小球离开平台做平抛运动,由h=$\frac{1}{2}$gt2得,t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×1.5}{10}}$=$\frac{\sqrt{30}}{10}$s
则落地时竖直方向上的分速度 vy=gt=10×$\frac{\sqrt{30}}{10}$=$\sqrt{30}$m/s.
据题:小球落地时的速度方向与水平方向成60°角,则有
tan60°=$\frac{{v}_{y}}{{v}_{0}}$,解得 v0=$\sqrt{10}$m/s.
所以弹簧被压缩时具有的最大弹性势能 EP=$\frac{1}{2}m{v}_{0}^{2}$=$\frac{1}{2}×2×(\sqrt{10})^{2}$=10J
小球落地点到桌子边缘的距离是 x=v0t=$\sqrt{30}$m,故A正确,BCD错误;
故选:A
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.平抛运动的时间由高度决定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.关于人造地球卫星,下列说法哪些是错误的( )
| A. | 发射卫星时,运载火箭飞行的最大速度必须达到或超过第一宇宙速度,发射才有可能成功 | |
| B. | 卫星绕地球做圆周运动时,其线速度一定不会小于第一宇宙速度 | |
| C. | 卫星绕地球做圆周运动的周期只要等于24小时,这个卫星一定相对于地面“定点” | |
| D. | 发射一个地球同步卫星,可以使其“定点”于西安市的正上方 |
11. 如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )
如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )
 如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )
如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )| A. | 卫星S的轨道半径r=$\frac{{T}^{2}gsi{n}^{2}θ}{4{π}^{2}}$ | |
| B. | 卫星S的速度大小v=$\frac{Tg}{4π}$sin2$\frac{θ}{2}$ | |
| C. | 地球的密度为$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$ | |
| D. | 地球的第一宇宙速度大小为$\frac{Tg}{2π}$sin$\frac{θ}{2}$ |
17.如图所示,物体静止在斜面上,以下几种说法中正确的是( )


| A. | 物体受到的静摩擦力沿斜面向下 | |
| B. | 物体所受重力沿垂直于斜面的分力就是物体对斜面的压力 | |
| C. | 物体所受重力的大小等于斜面对它的静摩擦力和支持力这两个力的合力的大小 | |
| D. | 物体受到的支持力与物体所受重力沿垂直于斜面的分力不是一对平衡力 |
4. 如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )
如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )
 如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )
如图所示,一物体在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经过一段时间恒力F对物体做功为60J,此后撤掉力F,物体又回到出发点,在整个运动过程中下列说法正确的是( )| A. | 撤去外力时,物体的动能为60 J | |
| B. | 物体运动到最高点的过程中,重力做功为60 J | |
| C. | 物体回到出发点时,物体的动能为60 J | |
| D. | 物体回到出发点时,重力的功率出现最大值 |
14. 如图所示,质量为m1、长为L的木板置于光滑的水平面上,一质量为m的滑块(视为质点)放置在木板左端,滑块与木板间滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块.当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1、长为L的木板置于光滑的水平面上,一质量为m的滑块(视为质点)放置在木板左端,滑块与木板间滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块.当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
 如图所示,质量为m1、长为L的木板置于光滑的水平面上,一质量为m的滑块(视为质点)放置在木板左端,滑块与木板间滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块.当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1、长为L的木板置于光滑的水平面上,一质量为m的滑块(视为质点)放置在木板左端,滑块与木板间滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块.当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )| A. | 滑块克服摩擦力所做的功为f(L+s) | |
| B. | 其他条件不变的情况下,F越大,滑块与木板间产生的热量越多 | |
| C. | 木板满足关系:f(L+s)=$\frac{1}{2}$m1v22 | |
| D. | F(L+s)-fL=$\frac{1}{2}$mv12+$\frac{1}{2}$m1v22 |
1.关于运动物体所受的合力、合力的功、动能的变化,下列说法正确的是( )
| A. | 运动物体所受的合力不为零,合力必做功,物体的动能一定要变化 | |
| B. | 运动物体所受的合力为零,则物体的动能一定不变 | |
| C. | 运动物体的动能保持不变,则该物体所受合力一定为零 | |
| D. | 运动物体所受合力不为零,则该物体一定做变速运动 |
18.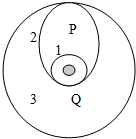 如图所示,发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后在轨道的Q点“点火”使卫星沿椭圆轨道2运行,当它经过椭圆轨道的远地点P时,再次“点火”,将卫星送入同步圆轨道3.卫星分别在轨道1、2、3上正常运行时(即不包括“点火”过程),下面的判断正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后在轨道的Q点“点火”使卫星沿椭圆轨道2运行,当它经过椭圆轨道的远地点P时,再次“点火”,将卫星送入同步圆轨道3.卫星分别在轨道1、2、3上正常运行时(即不包括“点火”过程),下面的判断正确的是( )
 如图所示,发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后在轨道的Q点“点火”使卫星沿椭圆轨道2运行,当它经过椭圆轨道的远地点P时,再次“点火”,将卫星送入同步圆轨道3.卫星分别在轨道1、2、3上正常运行时(即不包括“点火”过程),下面的判断正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后在轨道的Q点“点火”使卫星沿椭圆轨道2运行,当它经过椭圆轨道的远地点P时,再次“点火”,将卫星送入同步圆轨道3.卫星分别在轨道1、2、3上正常运行时(即不包括“点火”过程),下面的判断正确的是( )| A. | 卫星在轨道3上运行时的速率大于在轨道1上运行时的速率 | |
| B. | 卫星在轨道3上运行时的角速度小于在轨道1上运行时的角速度 | |
| C. | 卫星在轨道1上运行经过Q时的加速度等于在轨道2上运行经过P点时的加速度 | |
| D. | 卫星在轨道2上运行经过Q时的加速度等于在轨道2上运行经过P点时的加速度 |
19.下列说法正确的是( )
| A. | 体积大的物体一定不能看成质点 | B. | 加速度大,速度变化一定快 | ||
| C. | 速度方向与加速度方向一定相同 | D. | 加速度增大,速度一定增大 |