题目内容
11. 如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )
如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对卫星S的张角为θ,地球质量分布均匀的球体,其表面重力加速度为g,引力常量为G,下列说法正确的是( )| A. | 卫星S的轨道半径r=$\frac{{T}^{2}gsi{n}^{2}θ}{4{π}^{2}}$ | |
| B. | 卫星S的速度大小v=$\frac{Tg}{4π}$sin2$\frac{θ}{2}$ | |
| C. | 地球的密度为$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$ | |
| D. | 地球的第一宇宙速度大小为$\frac{Tg}{2π}$sin$\frac{θ}{2}$ |
分析 根据几何关系求得卫星轨道半径,根据万有引力提供圆周运动向心力和万有引力等于重力求解.
解答 解:A、由题意令卫星的轨道半径为r,地球的半径为R,根据几何关系可知,
r=$\frac{R}{sin\frac{θ}{2}}$ ①
根据万有引力提供向心力得:$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r ②
T=2π $\sqrt{\frac{{r}^{3}}{GM}}$ ③
根据万有引力等于重力,有:$\frac{GMm}{{R}^{2}}$=mg ④
联立解得:R=$\frac{{{gT}^{2}si{n}^{3}(\frac{θ}{2})}^{\;}}{{4π}^{2}}$⑤,r=$\frac{{{gT}^{2}si{n}^{2}(\frac{θ}{2})}^{\;}}{{4π}^{2}}$ ⑥
故A错误;
B、卫星S的速度大小为:v=$\frac{2πr}{T}$=$\frac{Tg}{2π}$sin2$\frac{θ}{2}$,故B错误;
C、地球的质量:M=ρV ⑦
联立④⑤⑦得:ρ=$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$.故C正确;
D、根据万有引力提供向心力得:
mg=m$\frac{{v}^{2}}{R}$
v=$\sqrt{gR}$=$\frac{Tg}{2π}$$\sqrt{{sin}^{3}\frac{θ}{2}}$,故D错误.
故选:C
点评 解决本题的关键是能根据几何关系求得卫星轨道半径与地球半径的大小关系,这是学生容易出错的主要地方.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 没有外力对物体做功,物体就没有动能 | |
| B. | 重力对物体不做功,物体就没有重力势能 | |
| C. | 滑动摩擦力只能做负功 | |
| D. | 物体克服重力做功,物体的重力势能就增加 |
6. A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
 A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )
A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,先后撤去F1、F2后,两物体最终停下,它们的vt图象如图所示.已知两物体与水平面间的滑动摩擦力大小相等.则下列说法正确的是( )| A. | F1、F2大小之比为2:1 | |
| B. | F1、F2对A、B做功之比为1:2 | |
| C. | A、B质量之比为2:1 | |
| D. | 全过程中A、B克服摩擦力做功之比为2:1 |
9. 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )
 如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )
如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则正确的是(g=10m/s2)( )| A. | 弹簧最大弹性势能为10 J | B. | 弹簧最大弹性势能为15 J | ||
| C. | 运动时间为$\frac{{\sqrt{3}}}{10}$s | D. | 落地点到桌子边缘的距离是$\sqrt{3}$m |
 某战士在倾角为30°的山坡上进行投掷手榴弹训练.他从A点以某一初速度v0=15m/s沿水平方向投出手榴弹后落在B点,该型号手榴弹从拉动弹弦到爆炸需要5s的时间,空气阻力不计,(g=10m/s2)求:
某战士在倾角为30°的山坡上进行投掷手榴弹训练.他从A点以某一初速度v0=15m/s沿水平方向投出手榴弹后落在B点,该型号手榴弹从拉动弹弦到爆炸需要5s的时间,空气阻力不计,(g=10m/s2)求: 用图所示实验装置验证机械能守恒定律.通过电磁铁控制的小铁球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出AB之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.
用图所示实验装置验证机械能守恒定律.通过电磁铁控制的小铁球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出AB之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.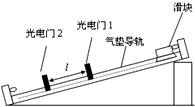 光电门是一种可以测量物体瞬时速度的器材
光电门是一种可以测量物体瞬时速度的器材