题目内容
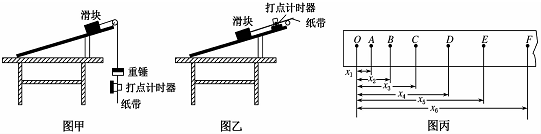
19. 如图所示,K是粒子发生器,D1、D2、D3是三块挡板,通过传感器可控制它们定时开启和关闭,D1、D2的间距为L,D2、D3的间距为$\frac{L}{2}$.在以O为原点的直角坐标系Oxy中有一磁感应强度大小为B,方向垂直纸面向里的匀强磁场,y轴和直线MN是它的左、右边界,且MN平行于y轴.现开启挡板D1、D3,粒子发生器仅在t=0时刻沿x轴正方向发射各种速率的粒子,D2仅在t=nT(n=0,1,2…,T为周期)时刻开启,在t=5T时刻,再关闭挡板D3,使粒子无法进入磁场区域.已知挡板的厚度不计,粒子质量为m、电荷量为+q(q大于0),不计粒子的重力,不计粒子间的相互作用,整个装置都放在真空中.
如图所示,K是粒子发生器,D1、D2、D3是三块挡板,通过传感器可控制它们定时开启和关闭,D1、D2的间距为L,D2、D3的间距为$\frac{L}{2}$.在以O为原点的直角坐标系Oxy中有一磁感应强度大小为B,方向垂直纸面向里的匀强磁场,y轴和直线MN是它的左、右边界,且MN平行于y轴.现开启挡板D1、D3,粒子发生器仅在t=0时刻沿x轴正方向发射各种速率的粒子,D2仅在t=nT(n=0,1,2…,T为周期)时刻开启,在t=5T时刻,再关闭挡板D3,使粒子无法进入磁场区域.已知挡板的厚度不计,粒子质量为m、电荷量为+q(q大于0),不计粒子的重力,不计粒子间的相互作用,整个装置都放在真空中.(1)求能够进入磁场区域的粒子的速度大小;
(2)已知从原点O进入磁场中速度最小的粒子经过坐标为(0,2)的P点,应将磁场边界MN在Oxy平面内如何平移,才能使从原点O进入磁场中速度最大的粒子经过坐标为($3\sqrt{3}$,6 )的Q点?
分析 (1)粒子必须在D3关闭前进入磁场才行,粒子由D1到D2和由D2到D3都是匀速直线运动,可得运动时间表达式,两段时间之和应小于等于5T,可解得能够进入磁场区域的粒子的速度.
(2)由进入磁场中速度最小的粒子经过坐标为(0cm,2cm)的P点可确定其轨道半径,进而确定最小速度;由(1)得到的速度表达式,可得最大速度,由速度关系可确定速度最大粒子的半径,做出运动轨迹图,由几何关系来判定该如何移动磁场的右边界MN.
解答 解:(1)设能够进入磁场区域的粒子的速度大小为vn,
由题意可知,粒子由D1到D2经历的时间为:△t1=$\frac{L}{{v}_{n}}$=nT (n=1、2…)
粒子由D2到D3经历的时间为:△t2=$\frac{L}{2{v}_{n}}$=$\frac{nT}{2}$,
t=5T时刻,挡板D3关闭,粒子无法进入磁场,故有△t=△t1+△t2≤5T,
解得:n≤$\frac{10}{3}$,即:n=1、2、3,
所以,能够进入磁场区域的粒子的速度为
所以,能够进入磁场区域的粒子的速度为:${v_n}=\frac{L}{nT}$(n=1、2、3);
(2)进入磁场中速度最小的粒子经过坐标为(0 cm,2 cm)的P点,所以R=1 cm.
粒子在磁场中做圆周运动,由牛顿第二定律得:$qvB=m\frac{v^2}{R}$,解得:$R=\frac{mv}{Bq}$,
由此可知,进入磁场中粒子的最大速度是最小速度的3倍,
故:R′=3R=3 cm,其圆心E坐标为(0,3 cm);
过Q点作圆轨迹的切线,设切点F的坐标为(x0,y0).
若此粒子在F点飞出磁场区域,它将沿直线FQ运动到Q点.
故F点一定在磁场的边界上.由图可知:
$tanθ=\frac{{3\sqrt{3}-{x_0}}}{{6-{y_0}}}$
$tanθ=\frac{{3-{y_0}}}{x_0}$,
由几何关系有:$x_0^2+{(3-{y_0})^2}={3^2}$
联立解得${x_0}=\frac{{3\sqrt{3}}}{2}cm$,${y_0}=\frac{3}{2}cm$
因此,只要将磁场区域的边界MN平行左移到:${x_0}=\frac{{3\sqrt{3}}}{2}cm$的F点,
速度最大的粒子在F点穿出磁场,将沿圆轨迹的切线方向到达Q点.
答:(1)能够进入磁场区域的粒子速度大小为:${v_n}=\frac{L}{nT}$(n=1、2、3)(n=1、2、3).
(2)已知从原点O进入磁场中速度最小的粒子经过坐标为(0cm,2cm)的P点,将磁场边界的MN平移到图中F点,才能使从原点O进入磁场中速度最大的粒子经过坐标为(3$\sqrt{3}$cm,6cm)的Q点.
点评 该题的关键点在于做速度最大粒子的轨迹图,带电粒子在磁场中运动,在混合场中的运动等问题,最重要的就是做出运动轨迹图,做这种图首先要能确定半径,其次要确定初末速度的方向.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案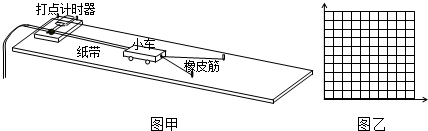
(1)实验时为了使小车只在橡皮筋作用下运动,应采取的措施是;
(2)每次实验得到的纸带上的点并不都是均匀的,为了测量小车获得的速度,应选用纸带的部分进行测量;
(3)下面是本实验的数据记录表,请将第2次、第3次…实验中橡皮筋做的功填写在对应的位置;
| 次数/数据/物理量 | 橡皮筋做的功Wn | 10个间隔的距离S、时间T | 小车速度vn | 小车速度平方vn2 | |
| 1 | W | 0.200m | 0.2s | 1.0 | 1.0 |
| 2 | 2W | 0.280m | 0.2s | 1.4 | 1.96 |
| 3 | 3W | 0.300m | 0.2s | 1.5 | 2.25 |
| 4 | 4W | 0.400m | 0.2s | 2.0 | 4.0 |
| 5 | 5W | 0.450m | 0.2s | 2.25 | |
(5)若在实验中你做出的图线与理论的推测不完全一致,你处理这种情况的做法是:分析误差来源或改进试验方案或测量手段,重新进行试验.
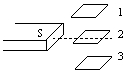 一水平放置的矩形线圈abcd在条形磁铁S极附近下落,在下落过程中,线圈平面保持水平,如图所示,位置1和3都靠近位置2,则线圈从位置1到位置2的过程中,线圈内有感应电流,线圈从位置2至位置3的过程中,线圈内有感应电流.(填:“有”或“无”)
一水平放置的矩形线圈abcd在条形磁铁S极附近下落,在下落过程中,线圈平面保持水平,如图所示,位置1和3都靠近位置2,则线圈从位置1到位置2的过程中,线圈内有感应电流,线圈从位置2至位置3的过程中,线圈内有感应电流.(填:“有”或“无”)
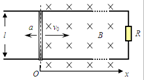 如图所示,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的一端接有阻值R=3Ω的电阻,在x≥0处有一垂直导轨平面向里的匀强磁场,磁感强度B=0.5T.一质量m=0.1kg,电阻r=2Ω的金属棒垂直搁在导轨上,并以v0=20m/s的初速度进入磁场,在水平拉力F的作用下作持续的匀变速直线运动,加速度大小a=2m/s2、方向与初速度方向相反.棒与导轨接触良好,其余电阻均不计.求:
如图所示,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的一端接有阻值R=3Ω的电阻,在x≥0处有一垂直导轨平面向里的匀强磁场,磁感强度B=0.5T.一质量m=0.1kg,电阻r=2Ω的金属棒垂直搁在导轨上,并以v0=20m/s的初速度进入磁场,在水平拉力F的作用下作持续的匀变速直线运动,加速度大小a=2m/s2、方向与初速度方向相反.棒与导轨接触良好,其余电阻均不计.求:

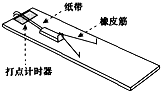 “探究功与物体速度变化的关系”的实验装置如图所示.
“探究功与物体速度变化的关系”的实验装置如图所示.