题目内容
4. 如图所示,长为L的细绳一端拴一质量为m小球,另一端固定在O点,绳的最大承受能力为11mg,在O点正下方O′点有一小钉,先把绳拉至水平再释放小球,为使绳不被拉断且小球能以O′为轴完成竖直面完整的圆周运动,则钉的位置到O点的距离为( )
如图所示,长为L的细绳一端拴一质量为m小球,另一端固定在O点,绳的最大承受能力为11mg,在O点正下方O′点有一小钉,先把绳拉至水平再释放小球,为使绳不被拉断且小球能以O′为轴完成竖直面完整的圆周运动,则钉的位置到O点的距离为( )| A. | 最小为$\frac{2}{5}$L | B. | 最小为$\frac{3}{5}$L | C. | 最大为$\frac{4}{5}$L | D. | 最大为$\frac{9}{10}$L |
分析 明确小球在整个过程中机械能守恒,当小球恰好能到达最高点时,此时距离最小,而小球在最低点时拉力最大时,此时距离最大,分别根据机械能守恒定律和向心力公式列式,联立即可求得钉子距悬点的距离.
解答 解:当小球恰好到达圆周运动的最高点时小球的转动半径为r,重力提供向心力,则有mg=m$\frac{{v}^{2}}{r}$;
根据机械能守恒定律可知,mg(L-2r)=$\frac{1}{2}$mv2
联立解得:r=$\frac{2}{5}$L,故钉的位置到O点的距离为L-$\frac{2}{5}$L=$\frac{3}{5}L$;
当小球转动时,恰好达到绳子的最大拉力时,即F=11mg,此时一定处在最低点,设半径为R,则有:
11mg-mg=m$\frac{{v}_{0}^{2}}{R}$
根据机械能守恒定律可知,mgL=$\frac{1}{2}$mv02
联立解得;R=$\frac{1}{5}L$,
故此时离最高点距离为$\frac{4}{5}$L,
则可知,距离最小为$\frac{3}{5}$L; 距离最大为$\frac{4}{5}$L;
故BC正确,AD错误.
故选:BC.
点评 本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力.小球摆到最低点虽与钉子相碰,但没有能量的损失.

练习册系列答案
相关题目
14.如下图所示是力学中的四个实验装置,其中哪些实验的物理思想方法相同( )
| A. |  观察桌面受力发生形变 | B. |  斜面滚球实验 | ||
| C. |  卡文迪放实验示意 图 | D. |  手的压力使玻璃瓶发生形变 |
15.关于平抛运动,下面说法正确的是( )
| A. | 由于速度的方向不断变化,因此平抛运动不是匀变速运动 | |
| B. | 由于物体只受重力作用,因此平抛运动是匀变速运动 | |
| C. | 平抛运动的水平位移由抛出时的高度和初速度的大小共同决定 | |
| D. | 平抛运动的时间由抛出时的高度和初速度的大小共同决定 |
12. 在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
 在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )
在如图所示的电路中,两个灯泡均发光,当滑动变阻器的滑动头向下滑动时,则( )| A. | 电源的输出功率增大 | B. | A灯和B灯都变亮 | ||
| C. | A灯变亮,B灯变暗 | D. | 电源的工作效率降低 |
9.在点电荷Q的电场中,有一点P,与点电荷Q的距离为r;现在P点放一电量为q的试探电荷,其受到的电场力为F,则P点的电场强度为( )
| A. | $\frac{F}{Q}$ | B. | $\frac{F}{q}$ | C. | k$\frac{Q}{{r}^{2}}$ | D. | k$\frac{q}{{r}^{2}}$ |
6. 一带正电的粒子仅在电场力作用下从A点经B、C运动到D点,其“速度-时间”图象如图所示.分析图象后,下列说法正确的是( )
一带正电的粒子仅在电场力作用下从A点经B、C运动到D点,其“速度-时间”图象如图所示.分析图象后,下列说法正确的是( )
 一带正电的粒子仅在电场力作用下从A点经B、C运动到D点,其“速度-时间”图象如图所示.分析图象后,下列说法正确的是( )
一带正电的粒子仅在电场力作用下从A点经B、C运动到D点,其“速度-时间”图象如图所示.分析图象后,下列说法正确的是( )| A. | B点的电势和电场强度一定都为零 | |
| B. | A处的电场强度大于C处的电场强度 | |
| C. | A点的电势小于B点的电势 | |
| D. | 粒子在A处的电势能小于在C处的电势能 |
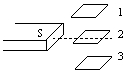 一水平放置的矩形线圈abcd在条形磁铁S极附近下落,在下落过程中,线圈平面保持水平,如图所示,位置1和3都靠近位置2,则线圈从位置1到位置2的过程中,线圈内有感应电流,线圈从位置2至位置3的过程中,线圈内有感应电流.(填:“有”或“无”)
一水平放置的矩形线圈abcd在条形磁铁S极附近下落,在下落过程中,线圈平面保持水平,如图所示,位置1和3都靠近位置2,则线圈从位置1到位置2的过程中,线圈内有感应电流,线圈从位置2至位置3的过程中,线圈内有感应电流.(填:“有”或“无”) 为了“探究外力做功与物体动能变化的关系”,查资料得知,弹簧的弹性势能Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.某同学就设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,既只有弹簧弹力做功.该同学设计实验如下:
为了“探究外力做功与物体动能变化的关系”,查资料得知,弹簧的弹性势能Ep=$\frac{1}{2}$kx2,其中k是弹簧的劲度系数,x是弹簧长度的变化量.某同学就设想用压缩的弹簧推静止的小球(质量为m)运动来探究这一问题.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,既只有弹簧弹力做功.该同学设计实验如下: