题目内容
2．
在篮球比赛中，某位同学获得罚球机会，他站在罚球线处用力将篮球投出，篮球约以1m/s的速度撞击篮筐．已知篮球质量约为0.6kg，篮筐离地高度约为3m，忽略篮球受到的空气阻力，则该同学罚球时对篮球做的功大约为（ ）| A． | 1J | B． | 10J | C． | 50J | D． | 100J |
分析 对篮球从手中出手到撞击篮筐的过程运用动能定理，求出罚球时对篮球做功的大小．
解答 解：对整个过程运用动能定理得，$W-mgh=\frac{1}{2}m{v}^{2}-0$，
代入数据解得W=$mgh+\frac{1}{2}m{v}^{2}$=$0.6×10×1.5+\frac{1}{2}×0.6×1$≈10J．
故选：B．
点评 本题考查了动能定理的基本运用，运用动能定理解题关键选择好研究的过程，分析过程中有哪些力做功，然后根据动能定理列式求解，注意代入数据时h不是0.3m，应该是球出手时到篮筐的大约高度．
练习册系列答案
相关题目
12．在匀强磁场中，一矩形金属线框绕与磁感线垂直的转动轴匀速转动，如图甲所示．产生的交变电动势随时间变化的规律如图乙所示．则下列说法正确的是（ ）
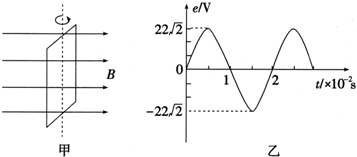
| A． | t=0.01s时穿过线框的磁通量最大 | |
| B． | 该交变电动势的有效值为11$\sqrt{2}$V | |
| C． | 该交变电动势的瞬时值表达式为e=22$\sqrt{2}$sin（100πt）V | |
| D． | 电动势瞬时值为22V时，线圈平面与中性面的夹角为45° |
如图所示，水平放置的圆盘绕通过它的中心的竖直轴匀速转动，质量为mA=40g的小盒A放在盘上，因盒很小略去其各边到O的距离差并且认为A距O点40cm，盒中有一小球B，B的质量mB=10g，不受盒内表面摩擦，在这种情况下．如A受盘的最大静摩擦力f=0.02N，为使A不相对圆盘滑动，盘转动的最大角速度ω是多大？这时球对盒壁的压力多大？
16．
如图所示，在菱形ABCD所在平面内有等量异种点电荷，AC、BD为对角线，O点为对角线交点．现让AC为电场中的一条等势线，下列说法正确的是（ ）
如图所示，在菱形ABCD所在平面内有等量异种点电荷，AC、BD为对角线，O点为对角线交点．现让AC为电场中的一条等势线，下列说法正确的是（ ）| A． | B、D两点场强大小一定相等 | B． | A、C两点场强大小一定相等 | ||
| C． | B、D两点电势可能相等 | D． | B、A间电势差与A、D间电势差相等 |
14．
足够长的粗糙斜面，倾角为θ，匀强电场垂直斜面向上，一带电小球质量为m，电量为+q，从静止出发（如图），小球开始运动后，以下正确的是（ ）
足够长的粗糙斜面，倾角为θ，匀强电场垂直斜面向上，一带电小球质量为m，电量为+q，从静止出发（如图），小球开始运动后，以下正确的是（ ）| A． | 小球一定沿斜面做匀加速直线运动 | |
| B． | 小球一定做匀加速直线运动，但不一定沿斜面 | |
| C． | 当E=$\frac{mgcosθ}{q}$时，小球不受斜面的摩擦力 | |
| D． | 只有Eq＞mg小球就离开斜面 |
11．
如图，竖直放置的光滑圆弧型轨道，O为圆心，AOB为沿水平方向的直径，AB=2R．在A点以初速度v0沿AB方向平抛一小球a，若v0不同，则小球a平抛运动轨迹也不同．则关于小球在空中的运动，下列说法中正确的是（ ）
如图，竖直放置的光滑圆弧型轨道，O为圆心，AOB为沿水平方向的直径，AB=2R．在A点以初速度v0沿AB方向平抛一小球a，若v0不同，则小球a平抛运动轨迹也不同．则关于小球在空中的运动，下列说法中正确的是（ ）| A． | v0越大，小球a位移越大 | B． | v0越大，小球a空中运动时间越长 | ||
| C． | 若v0=$\sqrt{\frac{gR}{2}}$，小球a动能增加量最大 | D． | 若v0=$\sqrt{\frac{gR}{2}}$，小球a末动能最大 |
如图所示，光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接，BC为导轨的直径，与水平面垂直，导轨半径为R=40cm，一个质量为m=2kg的小球将弹簧压缩至A处．小球从A处由静止释放被弹开后，以速度v=5m/s经过B点进入半圆形轨道，之后向上运动恰能沿轨道运动到C点（g取10m/s2），求：