题目内容
8．
如图所示，轻弹簧下悬挂一质量为m的物体，开始时物体静止在A处，现用竖直向下的恒力F=2mg向下拉物体，当物体运动到B处时，撤去外力F，此时物体的速度为v，已知A、B间的竖直距离为h．则物体从A运动到B的过程中，弹簧的弹性势能增加了（ ）| A． | 2mgh | B． | mgh+$\frac{1}{2}$mv2 | C． | 3mgh-$\frac{1}{2}$mv2 | D． | $\frac{1}{2}$mv2-mgh |
分析 物体从A运动到B的过程中，根据动能定理求出弹簧弹力做的功，从而求出弹簧的弹性势能增加量．
解答 解：物体从A运动到B的过程中，根据动能定理得：
$（F+mg）h+{W}_{弹}=\frac{1}{2}m{v}^{2}$
解得：${W}_{弹}=\frac{1}{2}m{v}^{2}-3mgh$
弹簧的弹性势能增加量为：$△{E}_{P}=-{W}_{弹}=3mgh-\frac{1}{2}m{v}^{2}$
故选：C
点评 本题主要考查了动能定理的直接应用，知道弹簧弹性势能的变化量与弹力做功的关系，难度不大，属于基础题．
练习册系列答案
相关题目
3．
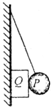如图所 示用轻绳将光滑小球P悬挂于竖直墙壁上，在墙壁和小球P之间夹着矩形物块Q，P、Q均处于静止状态，则下列说法正确的是（ ）
如图所 示用轻绳将光滑小球P悬挂于竖直墙壁上，在墙壁和小球P之间夹着矩形物块Q，P、Q均处于静止状态，则下列说法正确的是（ ）| A． | 物块Q受到3个力 | |
| B． | 物体P受4个力 | |
| C． | 若绳子变长，则绳子的拉力将变小 | |
| D． | 若绳子变短，则Q受到的静摩擦力将增大 |
如图所示，一个质量为m，带电量为q的微粒（重力忽略不计），从静止开始经U1电场加速后，垂直进入两平行金属板间的偏转电场，其电压U2=$\frac{{U}_{1}}{2}$，金属板长为L，两板间距d=$\frac{\sqrt{3}}{4}$L，求：
如图所示，半径为R的半圆柱形玻璃砖，放置在直角坐标系xOy中，圆心与坐标系原点O重合．在第二象限中坐标为（-1.5R，$\frac{\sqrt{3}}{2}$R）的点A处，放置一个激光器（圈中未画出），发出的一束细激光束a，激光束a平行于x轴射向玻璃砖．已知激光在玻璃砖中的折射率为$\sqrt{3}$．
20．物体以速度v匀速通过直线上的A、B两点，所用时间为t现在物体从A点由静止出发，先做匀加速直线运动（加速度为a1）到某一最大速度vm，然后立即做匀减速直线运动（加速度大小为a2）至B点速度恰好减为0，所用时间仍为t．则物体的（ ）
| A． | vm可为许多值，与al、a2的大小有关 | B． | vm可为许多值，与a1、a2的大小无关 | ||
| C． | a1、a2必须满足$\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{2v}{t}$ | D． | a1、a2必须是一定的 |
如图所示，传送带的水平部分AB长为L=5m，以v0=4m/s的速度顺时针转动，水平台面BC与传送带平滑连接于B点，BC长S=1m，台面右边有高为h=0.5m的光滑曲面CD，与BC部分相切于C点．一质量m=1kg的工件（视为质点），从A点无初速度释放，工件与传送带及台面BC间的动摩擦因数均为μ=0.2，g=10m/s2，求