题目内容
3. 如图所示,半径为R的半圆柱形玻璃砖,放置在直角坐标系xOy中,圆心与坐标系原点O重合.在第二象限中坐标为(-1.5R,$\frac{\sqrt{3}}{2}$R)的点A处,放置一个激光器(圈中未画出),发出的一束细激光束a,激光束a平行于x轴射向玻璃砖.已知激光在玻璃砖中的折射率为$\sqrt{3}$.
如图所示,半径为R的半圆柱形玻璃砖,放置在直角坐标系xOy中,圆心与坐标系原点O重合.在第二象限中坐标为(-1.5R,$\frac{\sqrt{3}}{2}$R)的点A处,放置一个激光器(圈中未画出),发出的一束细激光束a,激光束a平行于x轴射向玻璃砖.已知激光在玻璃砖中的折射率为$\sqrt{3}$.①作出光束a通过玻璃砖的光路图;
②求出激光束a射出玻璃砖后与x轴交点的坐标.
分析 作出激光束a射出玻璃砖后的光路,根据几何知识求解与x轴交点的坐标.
解答 解:作出激光束a射出玻璃砖后的光路,
由几何知识sinα=$\frac{\sqrt{3}R}{R}$
根据折射定律:$\frac{sinα}{sinβ}$=$\sqrt{3}$
又:y=$\frac{\sqrt{3}R}{2}$-Rsin(α-β)
解得:y=$\frac{\sqrt{3}-1}{2}$R
答:①作出光束a通过玻璃砖的光路图如图;
②求出激光束a射出玻璃砖后与x轴交点的坐标为(0,$\frac{\sqrt{3}-1}{2}$R).
点评 本题是几何光学问题,画出光路图,运用折射定律和几何知识结合进行求解,常规方法.

练习册系列答案
相关题目
18.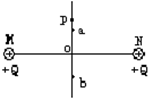 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
 M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )
M、N为两个等量同种电荷,在其连线的中垂线上P点由静止释放一个负点电荷-q,在电场力的作用下,-q将沿MN的中垂线PO穿过O点向下运动,在中垂线上取两点a、b,使oa=ob如图所示.若不计重力,则在释放负点电荷以后的运动过程中,下列说法正确的是( )| A. | 点电荷-q在a、b两点的速度一定相等 | |
| B. | 点电荷-q在a、b两点的动能一定相等 | |
| C. | 点电荷-q在a、b两点的加速度一定相等 | |
| D. | 点电荷-q做简谐运动 |
8. 如图所示,轻弹簧下悬挂一质量为m的物体,开始时物体静止在A处,现用竖直向下的恒力F=2mg向下拉物体,当物体运动到B处时,撤去外力F,此时物体的速度为v,已知A、B间的竖直距离为h.则物体从A运动到B的过程中,弹簧的弹性势能增加了( )
如图所示,轻弹簧下悬挂一质量为m的物体,开始时物体静止在A处,现用竖直向下的恒力F=2mg向下拉物体,当物体运动到B处时,撤去外力F,此时物体的速度为v,已知A、B间的竖直距离为h.则物体从A运动到B的过程中,弹簧的弹性势能增加了( )
 如图所示,轻弹簧下悬挂一质量为m的物体,开始时物体静止在A处,现用竖直向下的恒力F=2mg向下拉物体,当物体运动到B处时,撤去外力F,此时物体的速度为v,已知A、B间的竖直距离为h.则物体从A运动到B的过程中,弹簧的弹性势能增加了( )
如图所示,轻弹簧下悬挂一质量为m的物体,开始时物体静止在A处,现用竖直向下的恒力F=2mg向下拉物体,当物体运动到B处时,撤去外力F,此时物体的速度为v,已知A、B间的竖直距离为h.则物体从A运动到B的过程中,弹簧的弹性势能增加了( )| A. | 2mgh | B. | mgh+$\frac{1}{2}$mv2 | C. | 3mgh-$\frac{1}{2}$mv2 | D. | $\frac{1}{2}$mv2-mgh |
12.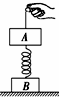 如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
 如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )
如图所示,质量相等的物体A、B通过一轻质弹簧相连,开始时B放在地面上,A、B均处于静止状态.现通过细绳将A向上缓慢拉起,第一阶段拉力做功为W1时,弹簧变为原长;第二阶段拉力再做功W2时,B刚要离开地面.弹簧一直在弹性限度内,则( )| A. | 两个阶段拉力做的功相等 | |
| B. | 拉力做的总功等于A的重力势能的增加量 | |
| C. | 第一阶段,拉力做的功大于A的重力势能的增加量 | |
| D. | 第二阶段,拉力做的功等于A的重力势能的增加量 |
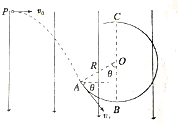 如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求:
如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求:
 如图所示,质量为M=4kg,长为L=1.5m的长木板,静止在光滑水平面上.一质量为m=1kg的小木块放在木板的左端,小木块与木板间的动摩擦因数μ=0.4,取g=10m/s2.
如图所示,质量为M=4kg,长为L=1.5m的长木板,静止在光滑水平面上.一质量为m=1kg的小木块放在木板的左端,小木块与木板间的动摩擦因数μ=0.4,取g=10m/s2. 如图所示是探究影响平行板电容器电容大小因素的实验装置.
如图所示是探究影响平行板电容器电容大小因素的实验装置.