��Ŀ����
1�� ��ͼ��ʾ��һ������Ϊm��������Ϊq�������������Բ��ƣ����Ӿ�ֹ��ʼ��U1�糡���ٺ�ֱ������ƽ�н�������ƫת�糡�����ѹU2=$\frac{{U}_{1}}{2}$�������峤ΪL��������d=$\frac{\sqrt{3}}{4}$L����
��ͼ��ʾ��һ������Ϊm��������Ϊq�������������Բ��ƣ����Ӿ�ֹ��ʼ��U1�糡���ٺ�ֱ������ƽ�н�������ƫת�糡�����ѹU2=$\frac{{U}_{1}}{2}$�������峤ΪL��������d=$\frac{\sqrt{3}}{4}$L������1��������ƫת�糡ʱ���ٶ�v0��С
��2�������ƫת�糡ʱ��ƫת�Ǧ�
��3��������ǿ�ų��Ŀ���ΪD��Ϊʹ�����Ӹôų��ұ��������Ÿ�Ӧǿ��B���ٶ��
���� ��1�������ڼ��ٵ糡�У��糡������ΪqU1���ɶ��ܶ�������ٶ�v0��
��2�����ӽ���ƫת�糡������ƽ���˶��������˶��ķֽⷨ������ţ�ٵڶ����ɡ��˶�ѧ���ٶȵķֽ����ƫת�Ǧȵ����У��ٵõ�ƫת�Ǧȣ�
��3�����ӽ���ų���������Բ���˶�����������������켣���ɼ���֪ʶ��뾶������B��
��� �⣺��1�����ڼ��ٵ糡���˶����̣��ɶ��ܶ����ã�
qU1=$\frac{1}{2}$mv02
��ã�v0=$\sqrt{\frac{2q{U}_{1}}{m}}$��
��2������ƫת�糡������ƽ���˶����У�
���ٶ�Ϊ��a=$\frac{q{U}_{2}}{md}$��
�ɳ��糡ʱ����ֱ���ٶ�Ϊ��vy=at
�˶�ʱ��Ϊ��t=$\frac{L}{{v}_{0}}$
�����ٶ�ƫת�ǵ�����Ϊ��tan��=$\frac{{v}_{y}}{{v}_{0}}=\frac{{U}_{2}L}{2{U}_{1}d}=\frac{\frac{1}{2}{U}_{1}L}{2{U}_{1}•\frac{\sqrt{3}}{4}L}=\frac{\sqrt{3}}{3}$
��ã���=30�㣻
��3������������ų�������Բ���˶������������ṩ����������������뾶ΪR��Ϊʹ�����Ӹôų��ұ��������켣��ͼ�� �ɼ��ι�ϵ֪
�ɼ��ι�ϵ֪
$R+\frac{1}{2}R=D$
���ԣ�R=$\frac{2}{3}D$
��������ų�ʱ���ٶ�Ϊv�䣬���У�$v��=\frac{{v}_{0}}{cos30��}=\frac{{2\sqrt{3}v}_{0}}{3}$
��ţ���˶����ɼ��˶�ѧ�����У�$qv��B=\frac{mv{��}^{2}}{R}$
�ã�$B=\frac{mv��}{qR}=\frac{m•\frac{2\sqrt{3}{v}_{0}}{3}}{q•\frac{2}{3}D}=\frac{\sqrt{3}m•\sqrt{\frac{2q{U}_{1}}{m}}}{qD}$=$\frac{1}{D}•\sqrt{\frac{6m{U}_{1}}{q}}$��
���������Ӳ�����ų����Ÿ�Ӧǿ��B����Ϊ$\frac{1}{D}•\sqrt{\frac{6m{U}_{1}}{q}}$��
�𣺣�1��������ƫת�糡ʱ���ٶ�v0��С��$\sqrt{\frac{2q{U}_{1}}{m}}$��
��2�������ƫת�糡ʱ��ƫת�Ǧ���30�㣮
��3�����������Ӳ�����ų����Ÿ�Ӧǿ��B����Ϊ$\frac{1}{D}•\sqrt{\frac{6m{U}_{1}}{q}}$��
���� �����Ǵ�����������ϳ����˶������⣬�ؼ��Ƿ������ӵ�����������˶����������ѧ�ķ���������

 ��У����ϵ�д�
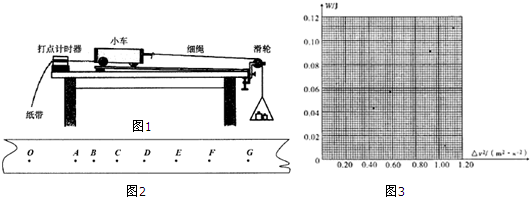
��У����ϵ�д���ijͬѧѡȡһ���Ƚ������ֽ����ͼ2�����з�����С���տ�ʼ�˶�ʱ��Ӧ��ֽ���ϵĵ��Ϊ��ʼ��O���ڵ㼣����������ѡȡ�߸�������A��B��C��D��E��F��G�����ڼ�������ʱ����Ϊ0.1s��������ʼ��O����������ľ��룬����������ӦС����˲ʱ�ٶȡ���������O��֮����ٶ�ƽ�����ʼ��O�������������ϸ����С�����Ĺ������м�����D����������û�м��㣬����ɼ��㲢�ѽ����������У�
| �㼣 | O | A | B | C | D | E | F | G |
| x/cm | 15.50 | 21.60 | 28.61 | 36.70 | 45.75 | 55.75 | 66.77 | |
| v/��m•s-1�� | -- | -- | 0.656 | 0.755 | -- | 0.953 | 1.051 | -- |
| ��v2/��m2•S-2�� | -- | 0.430 | 0.570 | 0.908 | 1.105 | -- | ||
| W/J | 0.432 | 0.0572 | 0.0915 | 0.112 |
�۸���ͼ������õ��Ľ���W���v2�����ȣ�
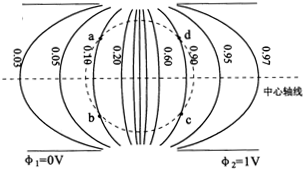 ��ͼ��ʾ��ʵ��Ϊ���ӻ���������۽��糡�еĵ����森a��b��c��dΪԲ�ϵ��ĸ���������˵������ȷ���ǣ�������
��ͼ��ʾ��ʵ��Ϊ���ӻ���������۽��糡�еĵ����森a��b��c��dΪԲ�ϵ��ĸ���������˵������ȷ���ǣ�������| A�� | a��b��c��d�ĵ�糡ǿ����ͬ | |
| B�� | һ���Ӵ�b���˶���c�㣬�糡�����Ĺ�Ϊ0.8eV | |
| C�� | ��һ���Ӵ�������������ߴ�Խ�糡���������ٶ��ȼ�С�����ӵ�ֱ���˶� | |
| D�� | ���д����ƽ�����������߽���糡����ĵ��ӣ���������Ҳ�ƽ�����������ߴ��� |
 ��ͼ��ʾ���ᵯ��������һ����Ϊm�����壬��ʼʱ���徲ֹ��A����������ֱ���µĺ���F=2mg���������壬�������˶���B��ʱ����ȥ����F����ʱ������ٶ�Ϊv����֪A��B�����ֱ����Ϊh���������A�˶���B�Ĺ����У����ɵĵ������������ˣ�������
��ͼ��ʾ���ᵯ��������һ����Ϊm�����壬��ʼʱ���徲ֹ��A����������ֱ���µĺ���F=2mg���������壬�������˶���B��ʱ����ȥ����F����ʱ������ٶ�Ϊv����֪A��B�����ֱ����Ϊh���������A�˶���B�Ĺ����У����ɵĵ������������ˣ�������| A�� | 2mgh | B�� | mgh+$\frac{1}{2}$mv2 | C�� | 3mgh-$\frac{1}{2}$mv2 | D�� | $\frac{1}{2}$mv2-mgh |
 һ�����ѹ��ԭ������Ȧ������nl��n2=11��5��ԭ��Ȧ�����ҽ����Դ���ӣ������ѹU��ͼ��ʾ������Ȧ������һ��10���ĵ��裮������
һ�����ѹ��ԭ������Ȧ������nl��n2=11��5��ԭ��Ȧ�����ҽ����Դ���ӣ������ѹU��ͼ��ʾ������Ȧ������һ��10���ĵ��裮������| A�� | ��������ĵ�����20 A | |
| B�� | ����貢���ĵ�ѹ����ʾ����100$\sqrt{2}$V | |
| C�� | ��ѹ�������빦����1��l03W | |
| D�� | ����1���ӵ��跢����������6��103 J |
 ��һͭƬ��һпƬ�ֱ����һֻƻ���ڣ�������һ���ġ�ˮ����ء�����綯��ԼΪ1.5V���������ֵ�ز����ܵ����ֵ�Ͳ�ϵĶ��ѹΪ1.5V�������Ϊ0.3A��С���ݣ�ԭ��������С���ݵĵ���̫С�ˣ���ʵ���û�����3mA����Ҫ�������̺��ʵĵ�ѹ��������ϴ��������������С���Լ����������������ء����ߵ�ʵ�����ľ���ȷ�زⶨˮ����صĵ綯��E������r��
��һͭƬ��һпƬ�ֱ����һֻƻ���ڣ�������һ���ġ�ˮ����ء�����綯��ԼΪ1.5V���������ֵ�ز����ܵ����ֵ�Ͳ�ϵĶ��ѹΪ1.5V�������Ϊ0.3A��С���ݣ�ԭ��������С���ݵĵ���̫С�ˣ���ʵ���û�����3mA����Ҫ�������̺��ʵĵ�ѹ��������ϴ��������������С���Լ����������������ء����ߵ�ʵ�����ľ���ȷ�زⶨˮ����صĵ綯��E������r��

 ��ͼ��ʾ����ǿ�ų�������ֱ���£��Ÿ�Ӧǿ�ȴ�СΪB���ڴų���ˮƽ�̶�һ��V���ͽ������CAD����֪��A=�ȣ������MN�ڿ���ϴ�A�㿪ʼ������F�����£��ش�ֱMN�������ٶ�v��������ƽ�ƣ�ƽ�ƹ����е�����Ϳ��ʼ�սӴ����ã��ҹ��ɵ��������λ�·����֪��������ܵIJ��Ϻͺ���������ͬ���䵥λ���ȵĵ����ΪR��������Ϳ�ܾ��㹻����������˶���ʼ����ų�����ֱ�����ڻ�·�еĵ���I���繦��P��ͨ����������ĵ���q������F���ĸ���������ʱ��t�ı仯��ϵͼ������ͼ����ȷ���ǣ�������
��ͼ��ʾ����ǿ�ų�������ֱ���£��Ÿ�Ӧǿ�ȴ�СΪB���ڴų���ˮƽ�̶�һ��V���ͽ������CAD����֪��A=�ȣ������MN�ڿ���ϴ�A�㿪ʼ������F�����£��ش�ֱMN�������ٶ�v��������ƽ�ƣ�ƽ�ƹ����е�����Ϳ��ʼ�սӴ����ã��ҹ��ɵ��������λ�·����֪��������ܵIJ��Ϻͺ���������ͬ���䵥λ���ȵĵ����ΪR��������Ϳ�ܾ��㹻����������˶���ʼ����ų�����ֱ�����ڻ�·�еĵ���I���繦��P��ͨ����������ĵ���q������F���ĸ���������ʱ��t�ı仯��ϵͼ������ͼ����ȷ���ǣ�������


