题目内容
19. 如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A、B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与A物块碰撞后立即以大小为$\frac{{v}_{0}}{3}$的速率弹回,在整个过程中物块A始终未滑离木板B且物块A可视为质点,求:
如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A、B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与A物块碰撞后立即以大小为$\frac{{v}_{0}}{3}$的速率弹回,在整个过程中物块A始终未滑离木板B且物块A可视为质点,求:①A相对B静止后的速度;
②木板B至少多长?
分析 ①根据小球m与物块A碰撞过程,以及A与B相互作用过程分别根据动量守恒定律列方程组求解即可;
②A在B上滑行的过程,根据能量的转化与守恒求解板长.
解答 解:①设小球m与物块A碰撞后A的速度为v1
设v0的方向为正方向,由动量守恒定律得 mv0=-m$•\frac{{v}_{0}}{3}$+2mv1
设物块A与木块B共同的速度v2.
由动量守恒定律得 2mv1=(2m+4m)v2.
解上两式可得 v1=$\frac{2}{3}{v}_{0}$,v2=$\frac{2}{9}{v}_{0}$
②设A在B上滑过的距离为L,由能的转化和守恒定律得
2μmgL=$\frac{1}{2}•$2mv12+$\frac{1}{2}$(2m+4m)v22.
解得 L=$\frac{4{v}_{0}^{2}}{27μg}$
答:
①A相对B静止后的速度是$\frac{2}{9}{v}_{0}$;
②木板B至少是$\frac{4{v}_{0}^{2}}{27μg}$.
点评 解决本题的关键是A与B组成的系统在碰撞过程中满足动量守恒,A在B上滑动时,A相对于B滑动的位移为相对位移,摩擦力在相对位移上做的功等于系统机械能的损耗.

练习册系列答案
相关题目
7.某一物体在质量不变的情况下,下列说法中正确的是( )
| A. | 物体动量改变,其速度大小一定改变 | |
| B. | 物体的速度方向改变,其动量不一定改变 | |
| C. | 物体做平抛运动时,在任意相等的时间内动量的变化量相同 | |
| D. | 物体的动能不变,其动量可能改变 |
4.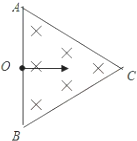 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | ||
| C. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
11. 如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
 如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )| A. | φA>φD>φC>φB | B. | EA>BD>EC>EB | C. | φA=φB>φC=φD | D. | EA=BB<EC=ED |
10. 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )| A. | 该弹簧振子的振幅为20cm | |
| B. | 该弹簧振子的周期为1s | |
| C. | 该弹簧振子的频率为2Hz | |
| D. | 振子从O点出发到再次回到O点的过程是一次全振动 |
 如图是用来验证动量守恒的实验装置,弹性球1用细线悬挂于O点,O点正下方桌子的边缘放有一静止弹性球2.实验时,将球1拉到A点并从静止开始释放球1,当它摆到悬点正下方时与球2发生对心碰撞.碰撞后,球1把处于竖直方向的轻质指示针OC推移到与竖直线最大夹角为β处,球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞时动量守恒.现已测出:在A点时,弹性球1球心离水平桌面的距离为a,轻质指示针OC与竖直方向的夹角为β,球1和球2的质量分别为m1、m2,C点与桌子边沿间的水平距离为b.
如图是用来验证动量守恒的实验装置,弹性球1用细线悬挂于O点,O点正下方桌子的边缘放有一静止弹性球2.实验时,将球1拉到A点并从静止开始释放球1,当它摆到悬点正下方时与球2发生对心碰撞.碰撞后,球1把处于竖直方向的轻质指示针OC推移到与竖直线最大夹角为β处,球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞时动量守恒.现已测出:在A点时,弹性球1球心离水平桌面的距离为a,轻质指示针OC与竖直方向的夹角为β,球1和球2的质量分别为m1、m2,C点与桌子边沿间的水平距离为b.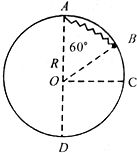 一个质量m=0.2kg的小球系于轻质弹簧的一端,且套在光滑竖直的圆环上的B点,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.5m,劲度系数为k=4.8N/m.如图所示,若小球从图中所示位置B点由静止开始滑动最低点D的过程中小球经过C点时的速度为vc=2m/s,小球到D点的速度vD=3m/s,重力加速度g=10m/s2,$\sqrt{2}$=1.414.求:
一个质量m=0.2kg的小球系于轻质弹簧的一端,且套在光滑竖直的圆环上的B点,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.5m,劲度系数为k=4.8N/m.如图所示,若小球从图中所示位置B点由静止开始滑动最低点D的过程中小球经过C点时的速度为vc=2m/s,小球到D点的速度vD=3m/s,重力加速度g=10m/s2,$\sqrt{2}$=1.414.求: