题目内容
9. 如图是用来验证动量守恒的实验装置,弹性球1用细线悬挂于O点,O点正下方桌子的边缘放有一静止弹性球2.实验时,将球1拉到A点并从静止开始释放球1,当它摆到悬点正下方时与球2发生对心碰撞.碰撞后,球1把处于竖直方向的轻质指示针OC推移到与竖直线最大夹角为β处,球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞时动量守恒.现已测出:在A点时,弹性球1球心离水平桌面的距离为a,轻质指示针OC与竖直方向的夹角为β,球1和球2的质量分别为m1、m2,C点与桌子边沿间的水平距离为b.
如图是用来验证动量守恒的实验装置,弹性球1用细线悬挂于O点,O点正下方桌子的边缘放有一静止弹性球2.实验时,将球1拉到A点并从静止开始释放球1,当它摆到悬点正下方时与球2发生对心碰撞.碰撞后,球1把处于竖直方向的轻质指示针OC推移到与竖直线最大夹角为β处,球2落到水平地面上的C点.测出有关数据即可验证1、2两球碰撞时动量守恒.现已测出:在A点时,弹性球1球心离水平桌面的距离为a,轻质指示针OC与竖直方向的夹角为β,球1和球2的质量分别为m1、m2,C点与桌子边沿间的水平距离为b.(1)在此实验中要求m1大于m2(填大于,小于或等于);
(2)此外,还需要测量的量是球1 的摆长L和桌面离水平地面的高度h;
(3)根据测量的数据,该实验中动量守恒的表达式为m1$\sqrt{a}$=m1$\sqrt{L(1-cosβ)}$+$\frac{{m}_{2}b}{2\sqrt{h}}$.
分析 分析题意,明确实验原理,知道要验证动量守恒,就需要知道碰撞前后的动量,所以要测量12两个小球的质量,1球下摆过程机械能守恒,根据守恒定律列式求最低点速度;球1上摆过程机械能再次守恒,可求解碰撞后速度;碰撞后小球2做平抛运动,根据平抛运动的分位移公式求解碰撞后2球的速度,然后验证动量是否守恒即可.
解答 解:(1)为了防止碰后球1反弹,故球1的质量应大于球b的质量;
(2、3)要验证动量守恒,就需要知道碰撞前后的动量,所以要测量1、2两个小球的质量m1、m2,要通过平抛运动的分位移公式求解碰撞后2球的速度,所以要测量桌面高H;
小球1从A处下摆过程只有重力做功,机械能守恒,根据机械能守恒定律,有
m1ga=$\frac{1}{2}$m1v12
解得:v1=$\sqrt{2ga}$
碰撞后1小球上升到最高点的过程中,机械能守恒,根据机械能守恒定律,有
m2gLcosβ=$\frac{1}{2}$m2v22
解得:v2=$\sqrt{L(1-cosβ)}$
碰撞后小球2做平抛运动,
t=$\sqrt{\frac{2h}{g}}$
所以2球碰后速度v3=$\frac{x}{t}$=$\frac{b}{\sqrt{\frac{2h}{g}}}$,
所以该实验中动量守恒的表达式为:m1v1=m2v3+m1v2
带入数据得:m1$\sqrt{a}$=m1$\sqrt{L(1-cosβ)}$+$\frac{{m}_{2}b}{2\sqrt{h}}$
故实验需要测量的量为:球1的摆长,桌面离水平地面的高度H;表达式为m1$\sqrt{a}$=m1$\sqrt{L(1-cosβ)}$+$\frac{{m}_{2}b}{2\sqrt{h}}$
故答案为:(1)大于; (2)球1的摆长,桌面离水平地面的高度H;(3)m1$\sqrt{a}$=m1$\sqrt{L(1-cosβ)}$+$\frac{{m}_{2}b}{2\sqrt{h}}$
点评 本题考查验证动量守恒定律的实验; 要注意明确验证动量守恒定律中,要学会在相同高度下,水平射程来间接测出速度的方法;同时还利用机械能守恒定律进行分析.

 阅读快车系列答案
阅读快车系列答案| A. | 做曲线运动的物体速度方向时刻在改变,故曲线运动是变速运动 | |
| B. | 做曲线运动的物体,受到的合外力方向在不断改变 | |
| C. | 只要物体做圆周运动,它所受的合外力一定指向圆心 | |
| D. | 曲线运动一定是变速率运动 |
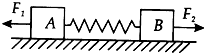 如图所示,水平轻弹簧与物体A和B相连,放在光滑水平面上,处于静止状态,物体A的质量为m,物体B的质量为M,且M>m.现用大小相等的水平恒力F1、F2拉A和B,从它们开始运动到弹簧第一次为最长的过程中( )
如图所示,水平轻弹簧与物体A和B相连,放在光滑水平面上,处于静止状态,物体A的质量为m,物体B的质量为M,且M>m.现用大小相等的水平恒力F1、F2拉A和B,从它们开始运动到弹簧第一次为最长的过程中( )| A. | 因F1=F2,所以A、B和弹簧组成的系统机械能守恒 | |
| B. | 因F1=F2,所以A、B和弹簧组成的系统动量守恒 | |
| C. | 由于F1、F2大小不变,所以m,M各自一直做匀加速运动 | |
| D. | 弹簧第一次最长时,A和B总动能最大 |
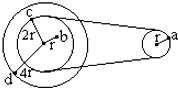 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )| A. | a点与b点的线速度大小相等 | |
| B. | a点与b点的角速度大小相等 | |
| C. | a点与c点的线速度大小相等 | |
| D. | a点的向心加速度小于d点的向心加速度 |
 在探究规格为“4.0V 2.OW”的小灯泡L的伏安特性曲线实验中,可供选用的器材如下:
在探究规格为“4.0V 2.OW”的小灯泡L的伏安特性曲线实验中,可供选用的器材如下: 在“验证机械能守恒定律”的实验中,所用电源的频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.若按实验要求正确地选出纸带进行测量,量得连续三点A、B、C到第一个点的距离如图所示(相邻计数点时间间隔为0.02s),那么:
在“验证机械能守恒定律”的实验中,所用电源的频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.若按实验要求正确地选出纸带进行测量,量得连续三点A、B、C到第一个点的距离如图所示(相邻计数点时间间隔为0.02s),那么: 如图所示,斜面ABC中AB段l1=2m且光滑,BC段l2=1m且粗糙,质量为1kg的小物块由A点以一定的初速度沿斜面向上滑行,到达B点速度vB=4m/s,到达C点速度为零,此过程中小物块在BC段速度的变化率是AB段的2倍,g=10m/s2,求:
如图所示,斜面ABC中AB段l1=2m且光滑,BC段l2=1m且粗糙,质量为1kg的小物块由A点以一定的初速度沿斜面向上滑行,到达B点速度vB=4m/s,到达C点速度为零,此过程中小物块在BC段速度的变化率是AB段的2倍,g=10m/s2,求: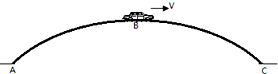 如图所示,是公路上的拱形桥,B是拱形桥的最高点,桥面的圆弧ABC所在圆的半径为R=400m. 现有一质量为m=2×103kg的汽车以恒定的功率P=3×106w过桥.在过最高点B时,汽车受牵引力F=3×105N.取g=10N/kg,小车视为质点,求:
如图所示,是公路上的拱形桥,B是拱形桥的最高点,桥面的圆弧ABC所在圆的半径为R=400m. 现有一质量为m=2×103kg的汽车以恒定的功率P=3×106w过桥.在过最高点B时,汽车受牵引力F=3×105N.取g=10N/kg,小车视为质点,求: 如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A、B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与A物块碰撞后立即以大小为$\frac{{v}_{0}}{3}$的速率弹回,在整个过程中物块A始终未滑离木板B且物块A可视为质点,求:
如图所示,在光滑的水平面上静止着一个质量为4m的木板B,B的左端静止着一个质量为2m的物块A,已知A、B之间的动摩擦因数为μ,现有质量为m的小球以水平速度v0飞来与A物块碰撞后立即以大小为$\frac{{v}_{0}}{3}$的速率弹回,在整个过程中物块A始终未滑离木板B且物块A可视为质点,求: