题目内容
9. 如图所示,一匝数N=10、总电阻为R=2.5Ω、边长L=0.3m的均质正三角形金属线框静置在粗糙水平面上,线段的顶点正好是半径r=$\frac{L}{3}$的圆形磁场的圆心,磁场方向竖直向下(正方向),磁感应强度大小B随时间t变化的关系如图乙所示,a、b是磁场边界与线框的两交点,已知线框与水平面间的最大静摩擦力f=0.6N,取π=3,则( )
如图所示,一匝数N=10、总电阻为R=2.5Ω、边长L=0.3m的均质正三角形金属线框静置在粗糙水平面上,线段的顶点正好是半径r=$\frac{L}{3}$的圆形磁场的圆心,磁场方向竖直向下(正方向),磁感应强度大小B随时间t变化的关系如图乙所示,a、b是磁场边界与线框的两交点,已知线框与水平面间的最大静摩擦力f=0.6N,取π=3,则( )| A. | t=0时穿过线框的磁通量为0.06Wb | |
| B. | 线框静止时,线框中的感应电流大小为0.6A | |
| C. | 线框静止时,a,b两点间电压为$\frac{1}{18}$V | |
| D. | 经时间t=0.8s,线框开始滑动 |
分析 通过磁通量的公式计算出t=0时的磁通量;
根据法拉第电磁感应定律,求得感应电动势大小,再依据闭合电路欧姆定律,求得感应电流的大小;
由楞次定律,与左手定则从而确定安培力方向,再依据F=NBIL,及矢量的合成法则,与几何关系,即可求解.
解答 解:A、t=0时穿过线框的磁通量为Φ=B×$\frac{1}{6}$πr2=2×$\frac{1}{6}×3×0.{1}^{2}$=0.01Wb,故A错误;
B、当线框静止时,根据法拉第电磁感应定律,则有:E=N$\frac{△B}{△t}$S=10×$\frac{5-2}{0.6}$×$\frac{1}{6}×3×0.{1}^{2}$=0.25V,
再由闭合电路欧姆定律,I=$\frac{E}{R}$=$\frac{0.25}{2.5}$=0.1A,故B错误;
C、由上可知,a,b两点间电压为U=IR′=0.1×$\frac{7}{9}×2.5$=$\frac{7}{36}$V,故C错误;
D、经时间t=0.8s,由图线可知,B=6T,依据B选项可知,感应电流I=0.1A,
则安培力大小F=NBIL=10×6×0.1×0.1=0.6N,
根据楞次定律可知,感应电流逆时针方向,由左手定则可知,安培力方向垂直导线框向外,如下图所示,
根据几何关系,可知,两安培力夹角为120°,则两安培力的合力为0.06N,
因已知线框与水平面间的最大静摩擦力f=0.6N,则开始滑动,故D正确.
故选:D.
点评 考查磁通量的公式,掌握法拉第电磁感应定律与闭合电路欧姆定律,注意左手定则与右手定则的区别,理解矢量的合成法则的应用.

练习册系列答案
相关题目
19.如图(甲)所示,一竖直放置的边长为L的正方形导线框,其内有垂直框面向外的均匀变化的磁场,磁场变化如图(乙)所示,导线框两端分别连平行板电容器的两极板M、N、M、N的长度和它们之间的距离都是d,两平行板所在平面与纸面垂直,一质子沿M、N两板正中央水平射入,恰好打在N板的中点处.已知质子的质量和电量分别为m、e(不考虑质子的重力).则( )


| A. | M、N两板间的电压U=$\frac{{B}_{0}{L}^{2}}{{t}_{0}}$ | B. | M、N两板间的电压U=B0L2t0 | ||
| C. | 质子入射的初速度v0=$\frac{L}{2}$$\sqrt{\frac{e{B}_{0}}{m{t}_{0}}}$ | D. | 质子入射的初速度v0=$\frac{d}{2{t}_{0}}$ |
17.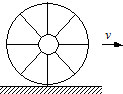 如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
 如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )| A. | 若车轮转速为3.75r/s,则观众觉得车轮是不动的 | |
| B. | 若车轮转速为30r/s,则观众觉得车轮是倒转的 | |
| C. | 若车轮转速为31r/s,则观众觉得车轮是倒转的 | |
| D. | 若车轮转速为29r/s,则观众觉得车轮是倒转的 |
20. 质量为m的小球在竖直平面内的圆管轨道内运动,小球的直径远小于圆管的直径,如图所示.已知小球以速度v通过最高点时对圆管的压力大小恰好为0,则小球以速度$\frac{v}{2}$通过圆管的最高点时( )
质量为m的小球在竖直平面内的圆管轨道内运动,小球的直径远小于圆管的直径,如图所示.已知小球以速度v通过最高点时对圆管的压力大小恰好为0,则小球以速度$\frac{v}{2}$通过圆管的最高点时( )
 质量为m的小球在竖直平面内的圆管轨道内运动,小球的直径远小于圆管的直径,如图所示.已知小球以速度v通过最高点时对圆管的压力大小恰好为0,则小球以速度$\frac{v}{2}$通过圆管的最高点时( )
质量为m的小球在竖直平面内的圆管轨道内运动,小球的直径远小于圆管的直径,如图所示.已知小球以速度v通过最高点时对圆管的压力大小恰好为0,则小球以速度$\frac{v}{2}$通过圆管的最高点时( )| A. | 小球对圆管的内、外壁均无压力 | B. | 小球对圆管的外壁压力等于$\frac{mg}{4}$ | ||
| C. | 小球对圆管的内壁压力等于$\frac{mg}{4}$ | D. | 小球对圆管的内壁压力等于$\frac{3mg}{4}$ |


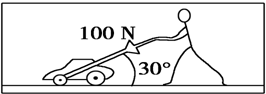 如图所示工人在推一台割草机,其推力F=100N,方向与水平面夹角为30°.
如图所示工人在推一台割草机,其推力F=100N,方向与水平面夹角为30°.