题目内容
9.某人骑摩托车在雾天匀速行驶,若能见度(观察者与能看见的最远目标间的距离)约为15m,设该人的反应时间为0.5s,已知摩托车刹车时产生的最大加速度为5m/s2,问:(1)为安全行驶,摩托车允许行驶的最大速度是多少?
(2)该人在反应时间0.5s内,摩托车的位移是多少?
分析 (1)为安全行驶,要保证摩托车在反应时间内和刹车后通过的总位移不能超过15m,由位移公式可求摩托车允许行驶的最大速度;
(2)该人在反应时间0.5s内汽车做匀速直线运动,利用速度公式可求摩托车的位移.
解答 解:(1)设为安全行驶,摩托车允许行驶的最大速度是v,则,
$x={v}_{0}t+\frac{0-{{v}_{0}}^{2}}{2a}$,即$15m={v}_{0}×0.5s+\frac{0-{{v}_{0}}^{2}}{2×(-5m/{s}^{2})}$,
解之得,v0=10m/s或v0=-15m/s(舍去).
故摩托车允许行驶的最大速度是10m/s.
(2)该人在反应时间0.5s内汽车做匀速直线运动,摩托车的位移:
x=v0t=10m/s×0.5s=5m.
答:(1)为安全行驶,摩托车允许行驶的最大速度是10m/s;
(2)该人在反应时间0.5s内,摩托车的位移是5m.
点评 (1)为安全行驶,要保证摩托车在反应时间内和刹车后通过的总位移不能超过15m,理解这一点是解答第一问的关键;(2)知道人在反应时间0.5s内汽车做匀速直线运动是解答第二问的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )
如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )
 如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )
如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )| A. | 整个运动过程中回路的最大电流为$\frac{{BL\sqrt{2gh}}}{R}$ | |
| B. | 整个运动过程中导体棒产生的焦耳热为mg(H+h)-$\frac{{{m^3}{g^2}{R^2}}}{{2{B^4}{L^4}}}$ | |
| C. | 整个运动过程中导体棒克服安培力所做的功为mgH | |
| D. | 整个运动过程中回路电流的功率为${({\frac{mg}{BL}})^2}R$ |
20.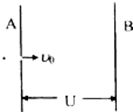 如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
 如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )| A. | 初速度为$\frac{{V}_{0}}{2}$,电压为$\frac{U}{2}$ | B. | 初速度为$\frac{{V}_{0}}{2}$,电压U不变 | ||
| C. | 初速度为V0,电压为$\frac{U}{2}$ | D. | 初速度为V0,电压为$\sqrt{2}$U |
17.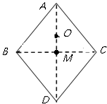 如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
 如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )| A. | A处与D处的场强相同 | |
| B. | 若再在A处固定电量为-Q的点电荷,则O处的场强大小为$\frac{9KQ}{{L}^{2}}$ | |
| C. | 若点电荷-Q从A静止释放,则经过M时速度最大 | |
| D. | 若点电荷+Q从B右侧靠近B的某点静止释放,沿BC向右运动过程加速度先增大后减小 |
4. 如图,在P板附近有一电子由静止开始向Q板运动.已知两极板间电势差为U,板间距为d,电子质量为m,电量为e.则关于电子在两板间的运动情况,下列叙述正确的是( )
如图,在P板附近有一电子由静止开始向Q板运动.已知两极板间电势差为U,板间距为d,电子质量为m,电量为e.则关于电子在两板间的运动情况,下列叙述正确的是( )
 如图,在P板附近有一电子由静止开始向Q板运动.已知两极板间电势差为U,板间距为d,电子质量为m,电量为e.则关于电子在两板间的运动情况,下列叙述正确的是( )
如图,在P板附近有一电子由静止开始向Q板运动.已知两极板间电势差为U,板间距为d,电子质量为m,电量为e.则关于电子在两板间的运动情况,下列叙述正确的是( )| A. | 若将板间距为d增大一倍,则电子到达Q板的速率保持不变 | |
| B. | 若将板间距为d增大一倍,则电子到达Q板的速率也增大一倍 | |
| C. | 若将两极板间电势差U增大四倍,则电子到达Q板的时间保持不变 | |
| D. | 若将两极板间电势差U增大四倍,则电子到达Q板的时间减为一半 |
14. 如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
 如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )
如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上边缘有一个质量为m,带电量为+q的小球,由静止开始沿轨道运动,下 列说法正确的是( )| A. | 小球运动过程中机械能守恒 | |
| B. | 小球在轨道最低点时速度最大 | |
| C. | 小球在最低点对轨道的压力为mg+qE | |
| D. | 小球在最低点对轨道的压力为3(mg+qE) |
19. 如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带AB的长度L=16m,则物体从A到B需要的时间为( ) (g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带AB的长度L=16m,则物体从A到B需要的时间为( ) (g=10m/s2,sin37°=0.6,cos37°=0.8)
 如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带AB的长度L=16m,则物体从A到B需要的时间为( ) (g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带AB的长度L=16m,则物体从A到B需要的时间为( ) (g=10m/s2,sin37°=0.6,cos37°=0.8)| A. | 1.6s | B. | 2.1s | C. | $\frac{4\sqrt{5}}{5}$s | D. | 2s |
 如图所示,一条长为L的绝缘细线,上端固定,下端系一质量为m的带电小球,将它置于电场强度为E、方向水平向右的匀强电场中,当小球平衡时,悬线与竖直方向的夹角α=45°.小球处于平衡状态.试求:
如图所示,一条长为L的绝缘细线,上端固定,下端系一质量为m的带电小球,将它置于电场强度为E、方向水平向右的匀强电场中,当小球平衡时,悬线与竖直方向的夹角α=45°.小球处于平衡状态.试求: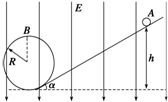 如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道下滑,已知小球的质量为m、电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力)
如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道下滑,已知小球的质量为m、电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力)