题目内容
8.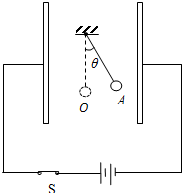 如图所示,平行板电容器与电源相连,两极板竖直放置,相距为d.在两极板的中央位置,用绝缘细线悬挂一个质量为m,电荷为q的小球.小球静止在A点,此时细线与竖直方向成θ角.已知电容器的电容为C,重力加速度大小为g.求:
如图所示,平行板电容器与电源相连,两极板竖直放置,相距为d.在两极板的中央位置,用绝缘细线悬挂一个质量为m,电荷为q的小球.小球静止在A点,此时细线与竖直方向成θ角.已知电容器的电容为C,重力加速度大小为g.求:(1)平行板电容器两极板间的电场强度大小;
(2)电容器极板上所带电荷量Q.
分析 (1)对小球受力分析,根据平衡条件可求得电场强度的大小;
(2)根据U=Ed可求得电势差,再根据电容器的定义式可求得电量大小.
解答  解:(1)带电小球静止在A点的受力如图:
解:(1)带电小球静止在A点的受力如图:
可得:Eq=mgtanθ;
解得:E=$\frac{mgtanθ}{q}$
(2)设两板间电压为U,则U=Ed 由C=$\frac{Q}{U}$
可得Q=UC
解得Q=CEd=$\frac{Cmgdtanθ}{q}$
答:(1)平行板电容器两极板间的电场强度大小为$\frac{mgtanθ}{q}$
(2)电容器极板上所带电荷量Q为$\frac{Cmgdtanθ}{q}$
点评 本题考查电容器以及电势差和电场强度之间的关系,要注意明确小球的受力分析规律,明确电场强度和电势差之间的关系,注意将电场力作为一种力进行分析求解即可.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
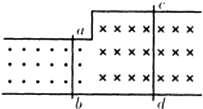
7. 边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
 边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )
边长为a的正方形处于有界磁场中,如图所示,一束电子有速度v0水平射入磁场后,分别从A处和C处射出,以下说法正确的是( )| A. | 从A处和C处射出的电子速度之比为2:1 | |
| B. | 从A处和C处射出的电子在磁场中运动的时间之比为2:1 | |
| C. | 从A处和C处射出的电子在磁场中运动周期之比为2:1 | |
| D. | 从A处和C处射出的电子在磁场中所受洛伦兹力之比为1:2 |
16. 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
 法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )
法拉第发现了电磁感应现象之后,又发明了世界上第一台发电机--法拉第圆盘发电机,揭开了人类将机械能转化为电能并进行应用的序幕.法拉第圆盘发电机的原理如图所示,将一个圆形铜盘放置在电磁铁的两个磁极之间(可视为磁感强度为B的匀强磁场),并使盘面与磁感线垂直,盘的边缘附近和中心分别装有与铜盘接触良好的电刷A、B(A、B间距离为L),两电刷与灵敏电流计相连.当铜盘绕中心轴按图示方向以角速度ω匀速转动时,则下面答案正确的是( )| A. | 由于穿过铜盘的磁通量不变,故灵敏电流计示数为0 | |
| B. | 盘面可视为无数辐条组成,任何时候都有磁条切割磁感线产生感应电动势 | |
| C. | 电刷A的电势高于电刷B的电势 | |
| D. | A、B间的感应电动势为E=BLω2 |
3.升降机的天花板上吊着弹簧秤,其下端吊着重20N的物体,当弹簧秤的示数为10N时,升降机的运动状态可能是( )
| A. | 正在匀速下降 | B. | 不可能上升 | ||
| C. | 以$\frac{g}{2}$的加速度匀减速上升 | D. | 以$\frac{g}{2}$加速度匀加速下降 |
 如图所示,金属棒ab是闭合电路的一部分,水平放置在竖直向下的匀强磁场中,现将金属棒以水平初速度v0向右抛出,设在整个过程中棒始终平动、与棒连接的细导线一直处于松弛状态,不计空气阻力.下列描述下落速度的水平分量大小vx、竖直分量大小vy与时间t的图象,可能正确的是( )
如图所示,金属棒ab是闭合电路的一部分,水平放置在竖直向下的匀强磁场中,现将金属棒以水平初速度v0向右抛出,设在整个过程中棒始终平动、与棒连接的细导线一直处于松弛状态,不计空气阻力.下列描述下落速度的水平分量大小vx、竖直分量大小vy与时间t的图象,可能正确的是( )



 如图所示,两根质量均为2kg的金属棒ab、cd静止放在光滑的水平导轨上,左、右两部分导轨间距之比为1:2,导轨间有强度相等、方向相反的匀强磁场,两棒的电阻之比Rab:Rcd=1:2,导轨足够长且电阻忽略不计.若用250N的水平力向右拉cd棒,在cd棒开始运动0.5m的过程中,cd棒上产生的焦耳热为30J,cd棒运动0.5m后立即撤去拉力,这时两棒速度大小之比vab:vcd=1:2,求:
如图所示,两根质量均为2kg的金属棒ab、cd静止放在光滑的水平导轨上,左、右两部分导轨间距之比为1:2,导轨间有强度相等、方向相反的匀强磁场,两棒的电阻之比Rab:Rcd=1:2,导轨足够长且电阻忽略不计.若用250N的水平力向右拉cd棒,在cd棒开始运动0.5m的过程中,cd棒上产生的焦耳热为30J,cd棒运动0.5m后立即撤去拉力,这时两棒速度大小之比vab:vcd=1:2,求:
 如图所示,纸面内有一直角坐标系xOy,在第一象限内是沿x轴正方向、场强大小为E的匀强电场,在第二象限内是垂直于纸面向里的匀强磁场B(大小未知),在第三、第四象限内是垂直于纸面向外的匀强磁场B′(大小未知),一质量为m,电荷量为e的正粒子从无限靠近y轴的M点以速度v0沿MO方向射出,经x轴上的N点进入第四象限,而后从x轴负半轴N′点(与N点关于O点对称)进入第二象限,最后恰好似沿y轴正方向的速度打在y轴正半轴上,已知tan∠OMN=$\frac{1}{2}$,粒子重力不计,试求:
如图所示,纸面内有一直角坐标系xOy,在第一象限内是沿x轴正方向、场强大小为E的匀强电场,在第二象限内是垂直于纸面向里的匀强磁场B(大小未知),在第三、第四象限内是垂直于纸面向外的匀强磁场B′(大小未知),一质量为m,电荷量为e的正粒子从无限靠近y轴的M点以速度v0沿MO方向射出,经x轴上的N点进入第四象限,而后从x轴负半轴N′点(与N点关于O点对称)进入第二象限,最后恰好似沿y轴正方向的速度打在y轴正半轴上,已知tan∠OMN=$\frac{1}{2}$,粒子重力不计,试求: 如图所示,在两个水平放置的平行金属板之间有竖直向下的匀强电场,电场强度为E.在两板之间及右侧有垂直纸面向里的足够大匀强磁场,磁感应强度均为B.现有${\;}_{1}^{2}$H、${\;}_{2}^{4}$He两个带电粒子在同一竖直平面内,分别从左端以水平速度射入两平行板之间,恰好都做匀速直线运动,射入点相距d=$\frac{2mE}{e{B}^{2}}$,已知e为元电荷的电荷量,m为质量子质量,${\;}_{1}^{2}$H、${\;}_{2}^{4}$He的质量分别为2m、4m,不计重力和粒子间的作用力.要使两粒子离开平行金属板之间的区域后能够相遇,求两粒子射入平行板的时间差△t.(如需作图辅助解题,请将图一并画出)
如图所示,在两个水平放置的平行金属板之间有竖直向下的匀强电场,电场强度为E.在两板之间及右侧有垂直纸面向里的足够大匀强磁场,磁感应强度均为B.现有${\;}_{1}^{2}$H、${\;}_{2}^{4}$He两个带电粒子在同一竖直平面内,分别从左端以水平速度射入两平行板之间,恰好都做匀速直线运动,射入点相距d=$\frac{2mE}{e{B}^{2}}$,已知e为元电荷的电荷量,m为质量子质量,${\;}_{1}^{2}$H、${\;}_{2}^{4}$He的质量分别为2m、4m,不计重力和粒子间的作用力.要使两粒子离开平行金属板之间的区域后能够相遇,求两粒子射入平行板的时间差△t.(如需作图辅助解题,请将图一并画出)