题目内容
13.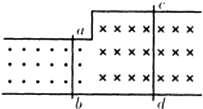 如图所示,两根质量均为2kg的金属棒ab、cd静止放在光滑的水平导轨上,左、右两部分导轨间距之比为1:2,导轨间有强度相等、方向相反的匀强磁场,两棒的电阻之比Rab:Rcd=1:2,导轨足够长且电阻忽略不计.若用250N的水平力向右拉cd棒,在cd棒开始运动0.5m的过程中,cd棒上产生的焦耳热为30J,cd棒运动0.5m后立即撤去拉力,这时两棒速度大小之比vab:vcd=1:2,求:
如图所示,两根质量均为2kg的金属棒ab、cd静止放在光滑的水平导轨上,左、右两部分导轨间距之比为1:2,导轨间有强度相等、方向相反的匀强磁场,两棒的电阻之比Rab:Rcd=1:2,导轨足够长且电阻忽略不计.若用250N的水平力向右拉cd棒,在cd棒开始运动0.5m的过程中,cd棒上产生的焦耳热为30J,cd棒运动0.5m后立即撤去拉力,这时两棒速度大小之比vab:vcd=1:2,求:(1)撤去外力时两棒的速度是多大?
(2)最终电路中产生的总的焦耳热是多少?
分析 (1)在有拉力F作用过程,cd棒上产生的焦耳热为Q=30J,根据焦耳定律和电阻之比,可求得ab棒上的产生热量Q′,根据功能关系和条件:vab:vcd=1:2列式,即可求得撤去F时,两棒的速度.在稳定运动时两棒产生的感应电动势相等,回路中感应电流为零,两棒都做匀速运动.撤去拉力F之后到最终稳定运动过程,运用动量定理,分别对两棒列式,即可求得两棒的最终速度vb,vc.
(2)根据能量守恒定律求解回路中产生的总焦耳热.再求ab棒中产生的总焦耳热Q.
解答 解:(1)由焦耳定律Q=I2Rt,I、t相等,Rab:Rcd=1:2,得两棒上产生的焦耳热之比 Qab:Qcd=1:2
可知ab棒上的生热为 Qab=$\frac{1}{2}$Qcd=$\frac{1}{2}$×30J=15J,
故Q=Qab+Qcd=45J
cd棒运动0.5m的过程中,由功能关系有:Fs=$\frac{1}{2}$mvab2+$\frac{1}{2}$mvcd2+Q
又F对cd做的功 W=Fs=250×0.5J=125J.
所以$\frac{1}{2}$mvab2+$\frac{1}{2}$mvcd2=80J
又vab:vcd=1:2,所以撤去外力时两棒的速度分别为:
vab=4m/s,vcd=8m/s
(2)由公式F=BIL知,任一时刻都有2Fab=Fcd,则2$\overline{{F}_{ab}}$=$\overline{{F}_{cd}}$
由动量定律得
对ab棒:$\overline{{F}_{ab}}$t=m(v′ab-vab)
对cd棒:-$\overline{{F}_{cd}}$t=m(v′cd-vcd)
在稳定运动时有:BLabv′ab=BLcdv′cd
且2Lab=Lcd,联立解得:v′cd=3.2m/s,v′ab=6.4m/s
所以电路中产生的总的焦耳热为:Q′=Fs-$\frac{1}{2}$mv′ab2-$\frac{1}{2}$mv′cd2
代入数据解得 Q′=73.8J
答:(1)撤去外力时两棒ab、cd的速度各是4m/s和8m/s.
(2)最终电路中产生的总的焦耳热是73.8J.
点评 本题是电磁感应与力学知识的综合应用,关键要抓住稳定时,两棒的感应电动势相等,都做匀速运动,运用动量定理求速度.

| A. | 相互接触并挤压的两物体间一定存在摩擦力 | |
| B. | 滑动摩擦力总是阻碍物体的运动 | |
| C. | 静止的物体也可以受到滑动摩擦力 | |
| D. | 只有静止的物体才受静摩擦力作用,运动的物体不会受静摩擦力作用 |
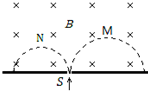 质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )| A. | M带正电,N带负电 | B. | M的速率大于N的速率 | ||
| C. | 洛仑兹力对M、N做正功 | D. | M、N的运行时间相等 |
 质量为m的物体在沿斜面向上的拉力F作用下沿放在水平地面上的质量为M的粗糙斜面匀加速下滑,此过程中斜面体保持静止.则地面对斜面( )
质量为m的物体在沿斜面向上的拉力F作用下沿放在水平地面上的质量为M的粗糙斜面匀加速下滑,此过程中斜面体保持静止.则地面对斜面( )| A. | 无摩擦力作用 | |
| B. | 有水平方向的摩擦力,但无法判定方向 | |
| C. | 支持力大小为(M+m)g | |
| D. | 支持力小于(M+m)g |

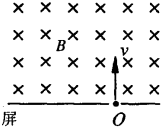 如图所示,匀强磁场的磁感应强度大小为B,方向垂直纸面向里,一个质量为m、电荷量为q的正离子,以速度v从小孔O射入匀强磁场,入射时速度方向既垂直于磁场方向,又与屏垂直,偏转后打在屏上S点(S点未在图上画出),求:
如图所示,匀强磁场的磁感应强度大小为B,方向垂直纸面向里,一个质量为m、电荷量为q的正离子,以速度v从小孔O射入匀强磁场,入射时速度方向既垂直于磁场方向,又与屏垂直,偏转后打在屏上S点(S点未在图上画出),求: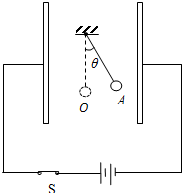 如图所示,平行板电容器与电源相连,两极板竖直放置,相距为d.在两极板的中央位置,用绝缘细线悬挂一个质量为m,电荷为q的小球.小球静止在A点,此时细线与竖直方向成θ角.已知电容器的电容为C,重力加速度大小为g.求:
如图所示,平行板电容器与电源相连,两极板竖直放置,相距为d.在两极板的中央位置,用绝缘细线悬挂一个质量为m,电荷为q的小球.小球静止在A点,此时细线与竖直方向成θ角.已知电容器的电容为C,重力加速度大小为g.求: 在某静电场中,将一个带电量为q=+2.0×10-9C的质点由a移到b点,电场力做功为2.0×10-5J,再把该电荷由b点移到c点,克服电场力做功6.0×10-5J.
在某静电场中,将一个带电量为q=+2.0×10-9C的质点由a移到b点,电场力做功为2.0×10-5J,再把该电荷由b点移到c点,克服电场力做功6.0×10-5J. 如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求:
如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根阻值未知质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin 37°=0.6,cos37°=0.8).求: