题目内容
18．
如图所示，两方向相反、磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC理想分开，三角形内磁场方向垂直纸面向里，三角形顶点A处有一质子源，能沿∠BAC的角平分线发射速度不同的质子（质子重力不计），所有质子均能通过C点，质子比荷$\frac{q}{m}$=k，则质子的速度可能为（ ）| A． | 2BkL | B． | $\frac{BkL}{2}$ | C． | $\frac{3BkL}{2}$ | D． | $\frac{BkL}{8}$ |
分析 质子在磁场中做匀速圆周运动，洛伦兹力提供向心力，根据题意作出质子可能的运动轨迹，应用牛顿第二定律求出质子在速度表达式，然后分析答题．
解答 解：质子带正电，且经过C点，其可能的轨迹如图所示：
所有圆弧所对圆心角均为60°，
所以质子运行半径：r=$\frac{L}{n}$（n=1，2，3，…），
质子在磁场中做圆周运动，洛伦兹力提供向心力，
由牛顿第二定律得：qvB=m$\frac{{v}^{2}}{r}$，
解得：v=$\frac{Bqr}{m}$=$\frac{BkL}{n}$（n=1，2，3，…），故AC错误，BD正确．
故选：BD．
点评 质子在匀强磁场中做匀速圆周运动洛伦兹力提供向心力，根据题意作出质子的运动轨迹是解题的关键，应用数学知识求出质子的可能轨道半径，应用牛顿第二定律求出质子的速度即可解题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
如图所示，为某透明介质的截面图，△AOC为等腰三角形，BC为半径R=12cm的四分之一圆弧，AB与水平屏幕MN垂直并接触于A点，一束红光射向圆心O，在AB分界面上的入射角i=45°，结果在水平屏幕MN上出现两个亮斑．已知该介质对红光的折射率为n=$\sqrt{2}$，求两个亮斑与A点间的距离分别为多少．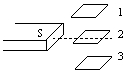
一水平放置的矩形线圈abcd在条形磁铁S极附近下落，在下落过程中，线圈平面保持水平，如图所示，位置1和3都靠近位置2，则线圈从位置1到位置2的过程中，线圈内有感应电流，线圈从位置2至位置3的过程中，线圈内有感应电流．（填：“有”或“无”）
6．
一带正电的粒子仅在电场力作用下从A点经B、C运动到D点，其“速度-时间”图象如图所示．分析图象后，下列说法正确的是（ ）
一带正电的粒子仅在电场力作用下从A点经B、C运动到D点，其“速度-时间”图象如图所示．分析图象后，下列说法正确的是（ ）| A． | B点的电势和电场强度一定都为零 | |
| B． | A处的电场强度大于C处的电场强度 | |
| C． | A点的电势小于B点的电势 | |
| D． | 粒子在A处的电势能小于在C处的电势能 |
某探究小组的同学利用直角三棱镜做光学实验，棱镜的横截面如图所示，α=30°，BC边长度为a．P为垂直于直线BC的光屏．现有一宽度等于AB边长度的平行单色光束垂直射向AB面，棱镜的折射率为$\sqrt{2}$，已知sin75°=$\frac{{\sqrt{6}+\sqrt{2}}}{4}$，cos75°=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$，求：
为了“探究外力做功与物体动能变化的关系”，查资料得知，弹簧的弹性势能Ep=$\frac{1}{2}$kx2，其中k是弹簧的劲度系数，x是弹簧长度的变化量．某同学就设想用压缩的弹簧推静止的小球（质量为m）运动来探究这一问题．为了研究方便，把小球放在水平桌面上做实验，让小球在弹力作用下运动，既只有弹簧弹力做功．该同学设计实验如下：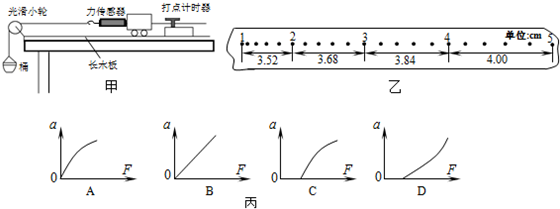
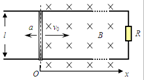如图所示，两条互相平行且足够长的光滑金属导轨位于水平面内，导轨间距l=0.2m，在导轨的一端接有阻值R=3Ω的电阻，在x≥0处有一垂直导轨平面向里的匀强磁场，磁感强度B=0.5T．一质量m=0.1kg，电阻r=2Ω的金属棒垂直搁在导轨上，并以v0=20m/s的初速度进入磁场，在水平拉力F的作用下作持续的匀变速直线运动，加速度大小a=2m/s2、方向与初速度方向相反．棒与导轨接触良好，其余电阻均不计．求：
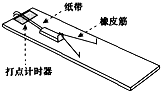“探究功与物体速度变化的关系”的实验装置如图所示．