��Ŀ����
10��ijͬѧ�������ͼ����ʾ��װ����̽��С���ļ��ٶ������ܺ����Ĺ�ϵ����װ������������С��������ˮƽ��ľ���ϣ�������СͰ�м���ϸɰ��ֱ��С���տ�ʼ�˶�Ϊֹ�����´����������ʾ��F0���Դ˱�ʾС������Ħ�����Ĵ�С���ٽ�С���Ż�ԭ������ס��������СͰ�м���ϸɰ�����´�������ʾ��F1��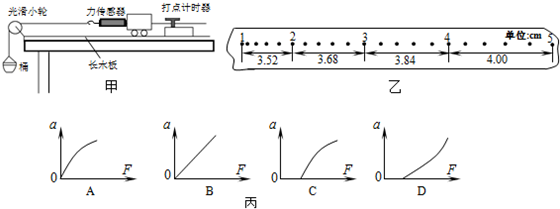
��1����ͨƵ��Ϊ50Hz�Ľ�����Դ���ͷ�С���������ͼ����ʾ��ֽ�����ӱȽ������ĵ���ÿ5����ȡһ�������㣬�������ڼ�����֮��ľ��룬��С���ļ��ٶ�a=0.16m/s2��
��2���ı�СͰ��ɰ������������ظ�ʵ�飬��ö������ݣ����С�����ٶ�a�����F
��F=F1-F0���Ĺ�ϵͼ����ֽ�����ʱ�����Ħ������ͼ����ͼ���п�����ȷ����B��
��3��ͬһ��ʵ���У�С���ͷ�ǰ������ʾ��F1��С�������˶�ʱ������ʾ��F2�Ĺ�ϵ��F1��F2��ѡ���������=����������
��4�����ڸ�ʵ�飬����˵������ȷ����D��
A��С���ʹ�������������ӦԶ����СͰ��ɰ��������
B��ʵ������Ҫ����ľ���Ҷ˵��
C��ʵ������Ҫ���С���ʹ�������������
D���ü�ɰ�ķ����ı������Ĵ�С��ҹ���ķ�����ȣ��ɸ�����ػ�ȡ����ʵ�����ݣ�
���� ��1�������ȱ���ֱ���˶������۹�ʽ��x=aT2����������ٶȵĴ�С��
��2���ı�СͰ��ɰ������������ظ�ʵ�飬��ö������ݣ����С�����ٶ�a�����F��F=F1-F0���Ĺ�ϵͼ�������Ѿ�ƽ��Ħ����������ͼ��Ӧ�ù�ԭ�㣻
��3����СͰ��������������ţ�ٵڶ�������⣻
��4���ڸ�ʵ����������������ֱ�ӵó����Ĵ�С��ʵ���в���Ҫ����ľ���Ҷ˵�ߣ���Ϊ�Ѿ�������С������Ħ�����Ĵ�С���ü�ɰ�ķ����ı������Ĵ�С��ҹ���ķ�����ȣ��ɸ�����ػ�ȡ����ʵ�����ݣ�
��� �⣺��1������ÿ��������������仹��4���㣬�������ڵļ�������ʱ����Ϊ��t=0.02��5=0.1s��
�����ȱ���ֱ���˶������۹�ʽ��x=at2�ɵü��ٶ�Ϊ��a=$\frac{{x}_{4}-{x}_{1}}{3{t}^{2}}$=$\frac{��4.00-3.52����1{0}^{-2}m}{3����0.1s��^{2}}$=0.16 m/s2��
��2���ı�СͰ��ɰ������������ظ�ʵ�飬��ö������ݣ����С�����ٶ�a�����F��F=F1-F0���Ĺ�ϵͼ��
�����Ѿ�ƽ��Ħ����������ͼ��Ӧ�ù�ԭ�㣬һ����б��ֱ�ߣ���B��ȷ��ACD����
��ѡ��B��
��3����СͰ������������СͰ����Ϊmg��
ľ���ͷ�ǰ���ɳӵ�ʾ��F1������F1=mg��
��С��������ΪMg��С���ڼ����˶�ʱ���ɳӵ�ʾ��F2��
����ţ�ٵڶ����ɵã�mg-F2=ma������F1��F2��
��4��A���ڸ�ʵ����������������ֱ�ӵó����Ĵ�С������ҪʹС���ʹ�������������ӦԶ����СͰ��ɰ������������A����
B��ʵ���в���Ҫ����ľ���Ҷ˵�ߣ���Ϊ�Ѿ�������С������Ħ�����Ĵ�С����B����
C��ʵ���в���Ҫ���С���ʹ���������������ֻ��Ҫ��֤С���ʹ����������������䣬��C����
D���ü�ɰ�ķ����ı������Ĵ�С��ҹ���ķ�����ȣ��ɸ�����ػ�ȡ����ʵ�����ݣ���D��ȷ��
��ѡ��D��
�ʴ�Ϊ����1��0.16����2��B����3��������4��D��
���� �������ʵ�鿼�����ȱ���ֱ�ߵĹ����Լ����۵�Ӧ�ã���ƽʱ��ϰ��Ҫ��ǿ����֪ʶ��������Ӧ�ã���߽���������������ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ��IJ�����������ݴ����Լ�ע���������ƽ��Ħ������ԭ���Լ�������ʵ����Ӧ�������

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д� ��ͼ��ʾ��ͼ����MNΪ�㹻��IJ����籡�����壬�ڽ�������Ҳ࣬����Ϊd��λ���Ϸ���һ�������Ϊ+q�ĵ���O�����ھ����Ӧ��������ͼ����ʾ�ĵ糡�ֲ���P�ǽ������ϵ�һ�㣬P�������O֮��ľ���Ϊr����λͬѧ�����P��ĵ糡ǿ�ȴ�С��������������ѣ���λͬѧ������ϸ�о�����ͼ����ʾ�ĵ糡�õ���һЩ��ʾ������������������֪����ͼ����ʾ�ĵ糡�ֲ���ͼ���������Ҳ�ĵ糡�ֲ���һ���ģ�ͼ��������ŵ��ɵ�����Ĵ�С��Ϊq������֮��ľ���Ϊ2d�����������������ߵ��д��ߣ��ɴ����Ƿֱ��P��ĵ糡ǿ�ȷ���ʹ�С���������жϣ�������ȷ���ǣ�������
��ͼ��ʾ��ͼ����MNΪ�㹻��IJ����籡�����壬�ڽ�������Ҳ࣬����Ϊd��λ���Ϸ���һ�������Ϊ+q�ĵ���O�����ھ����Ӧ��������ͼ����ʾ�ĵ糡�ֲ���P�ǽ������ϵ�һ�㣬P�������O֮��ľ���Ϊr����λͬѧ�����P��ĵ糡ǿ�ȴ�С��������������ѣ���λͬѧ������ϸ�о�����ͼ����ʾ�ĵ糡�õ���һЩ��ʾ������������������֪����ͼ����ʾ�ĵ糡�ֲ���ͼ���������Ҳ�ĵ糡�ֲ���һ���ģ�ͼ��������ŵ��ɵ�����Ĵ�С��Ϊq������֮��ľ���Ϊ2d�����������������ߵ��д��ߣ��ɴ����Ƿֱ��P��ĵ糡ǿ�ȷ���ʹ�С���������жϣ�������ȷ���ǣ�������| A�� | ������P��͵��ɵ���������СΪ $\frac{2kqd}{{r}^{3}}$ | |
| B�� | ������P��͵��ɵ���������СΪ $\frac{2kq\sqrt{{r}^{2}-{d}^{2}}}{{r}^{3}}$ | |
| C�� | ����ֱ�ڽ���������СΪ $\frac{2kqd}{{r}^{3}}$ | |
| D�� | ����ֱ�ڽ���������СΪ $\frac{2kq\sqrt{{r}^{2}-{d}^{2}}}{{r}^{3}}$ |
 ��ͼ��ʾ���������෴���Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų����߳�ΪL�ĵȱ�������ABC����ֿ����������ڴų�����ֱֽ����������ζ���A����һ����Դ�����ء�BAC�Ľ�ƽ���߷����ٶȲ�ͬ�����ӣ������������ƣ����������Ӿ���ͨ��C�㣬���ӱȺ�$\frac{q}{m}$=k�������ӵ��ٶȿ���Ϊ��������
��ͼ��ʾ���������෴���Ÿ�Ӧǿ�ȴ�С��ΪB����ǿ�ų����߳�ΪL�ĵȱ�������ABC����ֿ����������ڴų�����ֱֽ����������ζ���A����һ����Դ�����ء�BAC�Ľ�ƽ���߷����ٶȲ�ͬ�����ӣ������������ƣ����������Ӿ���ͨ��C�㣬���ӱȺ�$\frac{q}{m}$=k�������ӵ��ٶȿ���Ϊ��������| A�� | 2BkL | B�� | $\frac{BkL}{2}$ | C�� | $\frac{3BkL}{2}$ | D�� | $\frac{BkL}{8}$ |
 ��ͼ��ʾΪ�����ijһ����Q�����ĵ糡��a��b�ֱ�����糡�е����㣬����a�㴦�ĵ糡ǿ�ȴ�СEa=E0��b�㴦�ĵ糡ǿ�ȴ�СEb=3E0����Ea��Eb��ļнǴ���90�㣬������ͼ��ʾ��һ������ļ�����q�ڳ�����a�˶���b��������
��ͼ��ʾΪ�����ijһ����Q�����ĵ糡��a��b�ֱ�����糡�е����㣬����a�㴦�ĵ糡ǿ�ȴ�СEa=E0��b�㴦�ĵ糡ǿ�ȴ�СEb=3E0����Ea��Eb��ļнǴ���90�㣬������ͼ��ʾ��һ������ļ�����q�ڳ�����a�˶���b��������| A�� | a��b���㵽����Q�ľ���֮��ra��rb=3��1 | |
| B�� | a��b���㵽����Q�ľ���֮��ra��rb=$\sqrt{3}$��1 | |
| C�� | a��b���㴦�ĵ��ƵĴ�С��ϵΪ��a����b | |
| D�� | �ڰѼ�����q��ֱ�ߴ�a�Ƶ�b�Ĺ����У��糡������������������ |
 ��ͼ��ʾ����ֱֱ������ƽ��xoy����������ԭ�������OA��OB��x�������������ᶼ��45��ǣ���x���Ϸ���AOB�����ֲ��ŷ���ֱֽ�������СΪB1����ǿ�ų�����x����·������ŷ���ֱֽ�������СΪB2=$\frac{mv}{qL}$��ǿ�ų�������һ����Ϊm��������Ϊ+q�Ĵ����������ٶ�v��λ��ֱ��OA�ϵ�P��L��L������ֱ��������������������֣�������ÿ������ͬ��ʱ��T��ص�P�㣬����������������
��ͼ��ʾ����ֱֱ������ƽ��xoy����������ԭ�������OA��OB��x�������������ᶼ��45��ǣ���x���Ϸ���AOB�����ֲ��ŷ���ֱֽ�������СΪB1����ǿ�ų�����x����·������ŷ���ֱֽ�������СΪB2=$\frac{mv}{qL}$��ǿ�ų�������һ����Ϊm��������Ϊ+q�Ĵ����������ٶ�v��λ��ֱ��OA�ϵ�P��L��L������ֱ��������������������֣�������ÿ������ͬ��ʱ��T��ص�P�㣬���������������� ijʵ��С������ͼ��ʾʵ��װ��̽�����������붯�ܱ仯�Ĺ�ϵ������̨��ֱ�̶�������ˮƽ�����ϣ���ľ��һ�˷�����ˮƽ�����ԵP������һλ�÷���������̨��ֱ�����ϣ�ʹ��ľ����б���ã���ľ��P������һ����ţ��ù���ʱ����¼����ͨ�������ʱ����ʱ�䣬ʵ�鲽���ǣ�
ijʵ��С������ͼ��ʾʵ��װ��̽�����������붯�ܱ仯�Ĺ�ϵ������̨��ֱ�̶�������ˮƽ�����ϣ���ľ��һ�˷�����ˮƽ�����ԵP������һλ�÷���������̨��ֱ�����ϣ�ʹ��ľ����б���ã���ľ��P������һ����ţ��ù���ʱ����¼����ͨ�������ʱ����ʱ�䣬ʵ�鲽���ǣ�
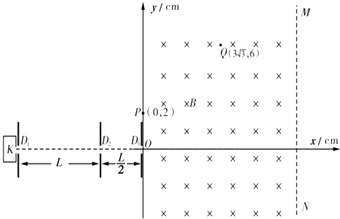 ��ͼ��ʾ��K�����ӷ�������D1��D2��D3�����鵲�壬ͨ���������ɿ������Ƕ�ʱ�����رգ�D1��D2�ļ��ΪL��D2��D3�ļ��Ϊ$\frac{L}{2}$������OΪԭ���ֱ������ϵOxy����һ�Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų���y���ֱ��MN���������ұ߽磬��MNƽ����y�ᣮ�ֿ�������D1��D3�����ӷ���������t=0ʱ����x����������������ʵ����ӣ�D2����t=nT��n=0��1��2����TΪ���ڣ�ʱ�̿�������t=5Tʱ�̣��ٹرյ���D3��ʹ����������ų�������֪����ĺ�Ȳ��ƣ���������Ϊm�������Ϊ+q��q����0�����������ӵ��������������Ӽ������ã�����װ�ö���������У�
��ͼ��ʾ��K�����ӷ�������D1��D2��D3�����鵲�壬ͨ���������ɿ������Ƕ�ʱ�����رգ�D1��D2�ļ��ΪL��D2��D3�ļ��Ϊ$\frac{L}{2}$������OΪԭ���ֱ������ϵOxy����һ�Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų���y���ֱ��MN���������ұ߽磬��MNƽ����y�ᣮ�ֿ�������D1��D3�����ӷ���������t=0ʱ����x����������������ʵ����ӣ�D2����t=nT��n=0��1��2����TΪ���ڣ�ʱ�̿�������t=5Tʱ�̣��ٹرյ���D3��ʹ����������ų�������֪����ĺ�Ȳ��ƣ���������Ϊm�������Ϊ+q��q����0�����������ӵ��������������Ӽ������ã�����װ�ö���������У�