题目内容
6.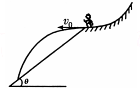 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,该战士落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,该战士落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 该战士在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| D. | 该战士刚要落到雪坡上时的速度大小是$\frac{{v}_{0}}{cosθ}$ |
分析 根据竖直位移和水平位移的关系,结合运动学公式求出运动的时间,通过水平位移分析落点的位置是否与初速度有关.根据速度时间公式求出竖直分速度,结合平行四边形定则求出战士落在斜坡上的速度.
解答 解:A、根据$tanθ=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得,该战士在空中经历的时间t=$\frac{2{v}_{0}tanθ}{g}$,则水平位移x=${v}_{0}t=\frac{2{{v}_{0}}^{2}tanθ}{g}$,初速度不同,运动时间不同,则水平位移不同,可知落在雪坡上的位置不同,由于平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,位移方向相同,则速度方向相同,故A、B错误,C正确.
D、战士落在斜坡上的竖直分速度vy=gt=2v0tanθ,根据平行四边形定则知,该战士落在斜坡上的速度v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}$=$\sqrt{{{v}_{0}}^{2}+4{{v}_{0}}^{2}ta{n}^{2}θ}$,故D错误.
故选:C.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,结合运动学公式和推论灵活求解.

练习册系列答案
相关题目
12. 如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面间没有相对滑动.则有( )
如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面间没有相对滑动.则有( )
 如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面间没有相对滑动.则有( )
如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面间没有相对滑动.则有( )| A. | 相同时间内,O1A、O2B转过的角度相等 | |
| B. | 相同时间内,A点通过的弧长等于B点通过的弧长 | |
| C. | B点的周期等于C点周期的两倍 | |
| D. | B点的转速等于C点转速的两倍 |
14. 如图所示,在光滑水平桌面上放着长为L的方木块M,今有A、B两颗子弹沿同一水平直线分别以vA、vB从M的两侧同时射入木块.A、B在木块中嵌入的深度分别为dA、dB,且dA<dB,(dA+dB)<L,而木块却一直保持静止,则可判断A、B子弹入射前( )
如图所示,在光滑水平桌面上放着长为L的方木块M,今有A、B两颗子弹沿同一水平直线分别以vA、vB从M的两侧同时射入木块.A、B在木块中嵌入的深度分别为dA、dB,且dA<dB,(dA+dB)<L,而木块却一直保持静止,则可判断A、B子弹入射前( )
 如图所示,在光滑水平桌面上放着长为L的方木块M,今有A、B两颗子弹沿同一水平直线分别以vA、vB从M的两侧同时射入木块.A、B在木块中嵌入的深度分别为dA、dB,且dA<dB,(dA+dB)<L,而木块却一直保持静止,则可判断A、B子弹入射前( )
如图所示,在光滑水平桌面上放着长为L的方木块M,今有A、B两颗子弹沿同一水平直线分别以vA、vB从M的两侧同时射入木块.A、B在木块中嵌入的深度分别为dA、dB,且dA<dB,(dA+dB)<L,而木块却一直保持静止,则可判断A、B子弹入射前( )| A. | 速度vA>vB | B. | 子弹A的动能小于B的动能 | ||
| C. | 子弹A的质量小于B的质量 | D. | 子弹A的动量大小等于B的动量大小 |
1.篮球运动员通常要伸出两臂迎接传来的篮球.接球时,两臂随球迅速收缩至胸前.这样做可以( )
| A. | 减小球对手的作用力 | B. | 减小球对手的冲量 | ||
| C. | 减小球的动量变化率 | D. | 减小球的动量变化量 |
18. 如图所示,一物体以角速度ω做匀速圆周运动,物理所受的向心力大小为F.则当物体从A点顺肘针运动半周到达B过程中,向心力的冲量大小和方向分别为( )
如图所示,一物体以角速度ω做匀速圆周运动,物理所受的向心力大小为F.则当物体从A点顺肘针运动半周到达B过程中,向心力的冲量大小和方向分别为( )
 如图所示,一物体以角速度ω做匀速圆周运动,物理所受的向心力大小为F.则当物体从A点顺肘针运动半周到达B过程中,向心力的冲量大小和方向分别为( )
如图所示,一物体以角速度ω做匀速圆周运动,物理所受的向心力大小为F.则当物体从A点顺肘针运动半周到达B过程中,向心力的冲量大小和方向分别为( )| A. | $\frac{πF}{ω}$,方向指向圆心 | B. | $\frac{2F}{ω}$,方向指向圆心 | ||
| C. | $\frac{πF}{ω}$,方向向左 | D. | $\frac{2F}{ω}$,方向向左 |
15. 如图所示,悬挂在天花板上的电风扇正常转动时,扇叶上P、Q两点绕轴做匀速圆周运动的线速度大小分别为vP、vQ,向心加速度大小分别为aP、aQ,则( )
如图所示,悬挂在天花板上的电风扇正常转动时,扇叶上P、Q两点绕轴做匀速圆周运动的线速度大小分别为vP、vQ,向心加速度大小分别为aP、aQ,则( )
 如图所示,悬挂在天花板上的电风扇正常转动时,扇叶上P、Q两点绕轴做匀速圆周运动的线速度大小分别为vP、vQ,向心加速度大小分别为aP、aQ,则( )
如图所示,悬挂在天花板上的电风扇正常转动时,扇叶上P、Q两点绕轴做匀速圆周运动的线速度大小分别为vP、vQ,向心加速度大小分别为aP、aQ,则( )| A. | vP>vQ,aP>aQ | B. | vP>vQ,aP<aQ | C. | vP<vQ,aP>aQ | D. | vP<vQ,aP<aQ |
 如图所示,光滑水平面上一辆小车右端紧靠固定的四分之一光滑圆弧轨道CD,小车表面与轨道最低点C相切,轨道半径R=0.5m.一质量为m=0.2kg的物块(可视为质点)以V0=10m/s初速度从左端滑上小车,已知小车长L=3.6m,物块与小车之间的动摩擦因数μ=0.5(g取10m/s2).求:
如图所示,光滑水平面上一辆小车右端紧靠固定的四分之一光滑圆弧轨道CD,小车表面与轨道最低点C相切,轨道半径R=0.5m.一质量为m=0.2kg的物块(可视为质点)以V0=10m/s初速度从左端滑上小车,已知小车长L=3.6m,物块与小车之间的动摩擦因数μ=0.5(g取10m/s2).求: 有一放在空气中透明的玻璃球,其折射率n=1.5、半径R=10cm,在玻璃球内有一离球心距离d=5cm的点光源S可向各个方向发光.已知真空中的光速c=3.0×108m/s.
有一放在空气中透明的玻璃球,其折射率n=1.5、半径R=10cm,在玻璃球内有一离球心距离d=5cm的点光源S可向各个方向发光.已知真空中的光速c=3.0×108m/s.