题目内容
15. 有一放在空气中透明的玻璃球,其折射率n=1.5、半径R=10cm,在玻璃球内有一离球心距离d=5cm的点光源S可向各个方向发光.已知真空中的光速c=3.0×108m/s.
有一放在空气中透明的玻璃球,其折射率n=1.5、半径R=10cm,在玻璃球内有一离球心距离d=5cm的点光源S可向各个方向发光.已知真空中的光速c=3.0×108m/s.①通过计算说明点光源发出的所有光都能够从玻璃球射出;
②求光线在玻璃球中的传播速度.
分析 ①若点光源发出的所有光都能够射出玻璃球,光源发出的所有光线都不会全反射,对于位置已固定的光源,d与R都是定值,当sinθ越大时,光线射出玻璃球的入射角α就越大,光线越容易发生全反射,当sinθ最大(θ=90°)时,不会发生全反射,根据临界角公式和数学正弦定理结合分析.
②根据公式v=$\frac{c}{n}$求光线在玻璃球中的传播速度.
解答  解:①如图,光源S发出的一条光线射到球面上的P点,由正弦定理得:$\frac{d}{sinα}$=$\frac{R}{sinθ}$
解:①如图,光源S发出的一条光线射到球面上的P点,由正弦定理得:$\frac{d}{sinα}$=$\frac{R}{sinθ}$
可得:sinα=$\frac{d}{R}$sinθ
对于位置已固定的光源,d与R都是定值,当sinθ越大时,光线射出玻璃球的入射角α就越大,光线越容易发生全反射,当sinθ最大(θ=90°)时有:sinα=$\frac{d}{R}$=$\frac{5}{10}$=0.5
设全反射临界角为C,则sinC=$\frac{1}{n}$=$\frac{2}{3}$
所以sinα<sinC,则光线在P点不发生全反射,点光源发出的所有光都能够从玻璃球射出;
②光线在玻璃球中的传播速度为 v=$\frac{c}{n}$=$\frac{3×1{0}^{8}}{1.5}$=2×108m/s
答:①见上;
②光线在玻璃球中的传播速度为2×108m/s.
点评 解决本题的关键是理解并掌握全反射条件,运用极限法确定临界条件,运用数学知识解答.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
6.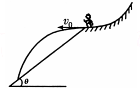 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,该战士落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,该战士落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 该战士在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| D. | 该战士刚要落到雪坡上时的速度大小是$\frac{{v}_{0}}{cosθ}$ |
6.动能相同的质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He),分别在两个匀强磁场区域Ⅰ和Ⅱ做匀速圆周运动,若区域Ⅱ的磁感应强度是区域Ⅰ的2倍,下列说法正确的是( )
| A. | 质子运动的速率是α粒子的$\sqrt{2}$倍 | |
| B. | 质子与α粒子做圆周运动的周期相等 | |
| C. | 质子与α粒子做圆周运动的半径相等 | |
| D. | 质子所受的洛伦兹力是α粒子的2倍 |
20.用电动轻质钢索将两个质量相同的攀岩运动员甲和乙匀速送上某个一定高度的岩顶,先后用较大速度和较小速度分别送甲、乙二人,则两种情况相比较,电动机的( )
| A. | 功率增加,总功不变 | B. | 功率减小,总功不变 | ||
| C. | 功率不变,总功减小 | D. | 功率减小,总功减小 |
7. 如图所示,电源E,导线,导电细软绳ab、cd,以及导体棒bc构成闭合回路,导电细软绳ab、cd的a端和d端固定不动,加上恰当的磁场后,当导体棒保持静止时,闭合回路中abcd所在平面与过ad的竖直平面成30°,已知ad和bc等长且都在水平面内,导体棒bc中的电流I=2A,导体棒的长度L=0.5m,导体棒的质量m=0.5kg,g取10m/s2,以下说法正确的是( )
如图所示,电源E,导线,导电细软绳ab、cd,以及导体棒bc构成闭合回路,导电细软绳ab、cd的a端和d端固定不动,加上恰当的磁场后,当导体棒保持静止时,闭合回路中abcd所在平面与过ad的竖直平面成30°,已知ad和bc等长且都在水平面内,导体棒bc中的电流I=2A,导体棒的长度L=0.5m,导体棒的质量m=0.5kg,g取10m/s2,以下说法正确的是( )
 如图所示,电源E,导线,导电细软绳ab、cd,以及导体棒bc构成闭合回路,导电细软绳ab、cd的a端和d端固定不动,加上恰当的磁场后,当导体棒保持静止时,闭合回路中abcd所在平面与过ad的竖直平面成30°,已知ad和bc等长且都在水平面内,导体棒bc中的电流I=2A,导体棒的长度L=0.5m,导体棒的质量m=0.5kg,g取10m/s2,以下说法正确的是( )
如图所示,电源E,导线,导电细软绳ab、cd,以及导体棒bc构成闭合回路,导电细软绳ab、cd的a端和d端固定不动,加上恰当的磁场后,当导体棒保持静止时,闭合回路中abcd所在平面与过ad的竖直平面成30°,已知ad和bc等长且都在水平面内,导体棒bc中的电流I=2A,导体棒的长度L=0.5m,导体棒的质量m=0.5kg,g取10m/s2,以下说法正确的是( )| A. | 磁场的最小值为2.5T,方向沿ba所在直线,由b指向a | |
| B. | 磁场的最小值为2.5T,方向沿ab所在直线,由a指向b | |
| C. | 磁场的最小值为$\frac{5\sqrt{3}}{3}$T,方向竖直向上 | |
| D. | 磁场的最小值为$\frac{5\sqrt{3}}{3}$T,方向竖直向下 |
4. 2017年05月05日14时许,中国自行研制、拥有完全自主知识产权的新一代大型喷气式干线客机C919从上海徐徐腾空,直冲云霄.预计下次试飞要飞机在一个半径为R的水平面内的圆周轨道上匀速飞行,如图所示飞机在飞行时,空气对飞机产生了一个向上的升力,下列说法正确的是( )
2017年05月05日14时许,中国自行研制、拥有完全自主知识产权的新一代大型喷气式干线客机C919从上海徐徐腾空,直冲云霄.预计下次试飞要飞机在一个半径为R的水平面内的圆周轨道上匀速飞行,如图所示飞机在飞行时,空气对飞机产生了一个向上的升力,下列说法正确的是( )
 2017年05月05日14时许,中国自行研制、拥有完全自主知识产权的新一代大型喷气式干线客机C919从上海徐徐腾空,直冲云霄.预计下次试飞要飞机在一个半径为R的水平面内的圆周轨道上匀速飞行,如图所示飞机在飞行时,空气对飞机产生了一个向上的升力,下列说法正确的是( )
2017年05月05日14时许,中国自行研制、拥有完全自主知识产权的新一代大型喷气式干线客机C919从上海徐徐腾空,直冲云霄.预计下次试飞要飞机在一个半径为R的水平面内的圆周轨道上匀速飞行,如图所示飞机在飞行时,空气对飞机产生了一个向上的升力,下列说法正确的是( )| A. | 飞机的重力与升力合力为零 | |
| B. | 飞机所受空气的升力沿斜向上方且偏向圆心一侧 | |
| C. | 飞机受到重力、升力、牵引力和空气阻力的作用,其合力为零 | |
| D. | 飞机受到重力、升力、牵引力、空气阻力和向心力的作用 |
5. 研究滑动摩擦力大小的实验装置如图所示,木块和木板叠放于水平桌面上,弹簧测力计水平固定,通过水平细绳与木块相连,用缓慢增大的力拉动木板,使之在桌面上滑动(木块始终未脱离木板).弹簧测力计示数稳定后( )
研究滑动摩擦力大小的实验装置如图所示,木块和木板叠放于水平桌面上,弹簧测力计水平固定,通过水平细绳与木块相连,用缓慢增大的力拉动木板,使之在桌面上滑动(木块始终未脱离木板).弹簧测力计示数稳定后( )
 研究滑动摩擦力大小的实验装置如图所示,木块和木板叠放于水平桌面上,弹簧测力计水平固定,通过水平细绳与木块相连,用缓慢增大的力拉动木板,使之在桌面上滑动(木块始终未脱离木板).弹簧测力计示数稳定后( )
研究滑动摩擦力大小的实验装置如图所示,木块和木板叠放于水平桌面上,弹簧测力计水平固定,通过水平细绳与木块相连,用缓慢增大的力拉动木板,使之在桌面上滑动(木块始终未脱离木板).弹簧测力计示数稳定后( )| A. | 由于木块相对桌面静止,弹簧测力计示数与木板的运动状态有关 | |
| B. | 由于木块相对桌面静止,弹簧测力计示数一定等于木板受到的拉力 | |
| C. | 由于木板相对桌面运动,弹簧测力计示数一定小于木板受到的拉力 | |
| D. | 由于木板相对桌面运动,弹簧测力计示数一定大于木板受到的滑动摩擦力 |
 如图所示,一半径为R=2m的圆环,以直径AB为轴匀速转动,转动周期T=2s,环上有M、N两点. M点的角速度ω=3.14rad/s.N点的线速度v=3.14 m/s.
如图所示,一半径为R=2m的圆环,以直径AB为轴匀速转动,转动周期T=2s,环上有M、N两点. M点的角速度ω=3.14rad/s.N点的线速度v=3.14 m/s. 如图所示,在倾角为θ的斜面上固定间距为d的两平行光滑金属导轨,上端连接一阻值为R的电阻,间距为L的三虚线段OO′、PP′、QQ′均水平且与金属导轨垂直,PP′、QQ′间有垂直斜面向上的匀强磁场.一长为d、质量为m、电阻为R的均匀导体棒从导.轨上OO′从静止开始释放,进入磁场时恰好匀速下滑.已知重力加速度为g.金属导轨电阻不计,求:
如图所示,在倾角为θ的斜面上固定间距为d的两平行光滑金属导轨,上端连接一阻值为R的电阻,间距为L的三虚线段OO′、PP′、QQ′均水平且与金属导轨垂直,PP′、QQ′间有垂直斜面向上的匀强磁场.一长为d、质量为m、电阻为R的均匀导体棒从导.轨上OO′从静止开始释放,进入磁场时恰好匀速下滑.已知重力加速度为g.金属导轨电阻不计,求: