题目内容
17.两个球都以2m/s的速度相向运动,其中一球的质量是另一球质量的3倍.它们相遇后粘合在一起,求它们共同的速度,这个过程中系统损失了百分之几的机械能?分析 由动量守恒定律可以求出它们的共同速度,由能量守恒定律可以求出损失的机械能.
解答 解:以其中一个质量大的球的速度的方向为正方向,两物体碰撞过程中动量守恒,设它们的质量分别为m和3m,碰撞后的速度为v′;
由动量守恒定律得:3mv-mv=(3m+m)v′,
代入数据解得:v′=1 m/s,
系统损失是机械能为:△E=$\frac{1}{2}$•3mv2+$\frac{1}{2}$mv2-$\frac{1}{2}$(3m+m)v′2=$\frac{3}{2}m{v}^{2}$;
故系统损失的机械能的百分比为:η=$\frac{△E}{E}$=$\frac{\frac{3}{2}m{v}^{2}}{\frac{1}{2}•3m{v}^{2}+\frac{1}{2}m{v}^{2}}×100$%=75%
答:它们的共同速度是1m/s,这个过程中系统损失了百分之75的机械能.
点评 本题考查了完全非弹性碰撞过程,应用动量守恒定律与能量守恒即可正确解题.

练习册系列答案
相关题目
3.关于力对物体做功,如下说法正确的是( )
| A. | 静摩擦力对物体可能做正功 | |
| B. | 作用力的功与反作用力的功其代数和一定为零 | |
| C. | 滑动摩擦力对物体一定做负功 | |
| D. | -对相互作用的滑动摩擦力的总功可能为零 |
4.物体从静止开始做匀加速直线运动,第3s内通过的位移是3m,下列说法正确的是( )
| A. | 第3 s内的平均速度是3 m/s | B. | 物体的加速度是1.2 m/s2 | ||
| C. | 前3 s内的位移是6 m | D. | 3 s末的速度是4m/s |
12.下列对经典力学、量子力学和相对论的说法正确的是( )
| A. | 在相对论中,物体的质量随运动速度而改变 | |
| B. | 量子力学适用于高速运动物体,相对论适用于微观粒子运动 | |
| C. | 经典力学理论普遍适用,大到天体,小到微观粒子均适用 | |
| D. | 相对论与量子力学否定了经典力学理论 |
2.2016年“科学突破奖”颁奖仪式在美国举行,我国科学家王贻芳获得“基础物理学突破奖”.在物理学的发展过程中,科学家们创造出了许多物理学研究方法,以下关于所用物理学研究方法的叙述正确的是( )
| A. | 牛顿第一定律是利用逻辑思维对事实进行分析的产物,能用实验直接验证 | |
| B. | 重心、合力和分力都体现了等效替换思想 | |
| C. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每小段近似看做匀速直线运动,然后把各个小段的位移相加,这里采用了理想模型法 | |
| D. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法是微元法 |
9. 如图所示,一个半径为r的水平圆盘上放着两个木块,木块M放在圆盘的边缘处,木块N放在离圆心$\frac{1}{3}$r处,用伸直轻质细线连接,木块M和N质量之比为1:3,且与圆盘摩擦因数为μ,现在水平圆盘从静止开始缓慢增加转速,到两物刚要相对圆盘滑动时,不再增加转速.取最大静摩擦力等于滑动摩擦力,下列说法中正确的是(M质量为m,重力加速度为g)( )
如图所示,一个半径为r的水平圆盘上放着两个木块,木块M放在圆盘的边缘处,木块N放在离圆心$\frac{1}{3}$r处,用伸直轻质细线连接,木块M和N质量之比为1:3,且与圆盘摩擦因数为μ,现在水平圆盘从静止开始缓慢增加转速,到两物刚要相对圆盘滑动时,不再增加转速.取最大静摩擦力等于滑动摩擦力,下列说法中正确的是(M质量为m,重力加速度为g)( )
 如图所示,一个半径为r的水平圆盘上放着两个木块,木块M放在圆盘的边缘处,木块N放在离圆心$\frac{1}{3}$r处,用伸直轻质细线连接,木块M和N质量之比为1:3,且与圆盘摩擦因数为μ,现在水平圆盘从静止开始缓慢增加转速,到两物刚要相对圆盘滑动时,不再增加转速.取最大静摩擦力等于滑动摩擦力,下列说法中正确的是(M质量为m,重力加速度为g)( )
如图所示,一个半径为r的水平圆盘上放着两个木块,木块M放在圆盘的边缘处,木块N放在离圆心$\frac{1}{3}$r处,用伸直轻质细线连接,木块M和N质量之比为1:3,且与圆盘摩擦因数为μ,现在水平圆盘从静止开始缓慢增加转速,到两物刚要相对圆盘滑动时,不再增加转速.取最大静摩擦力等于滑动摩擦力,下列说法中正确的是(M质量为m,重力加速度为g)( )| A. | 全程中M、N两木块的向心加速度大小相等 | |
| B. | 全程中M所受摩擦力小于N所受的摩擦力 | |
| C. | 全程中,圆盘对M、N做功为$\frac{2}{3}$μmgr | |
| D. | 全程中,圆盘对M、N做功为$\frac{5}{3}$μmgr |
6.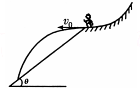 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,该战士落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,该战士落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 该战士在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| D. | 该战士刚要落到雪坡上时的速度大小是$\frac{{v}_{0}}{cosθ}$ |
6.动能相同的质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He),分别在两个匀强磁场区域Ⅰ和Ⅱ做匀速圆周运动,若区域Ⅱ的磁感应强度是区域Ⅰ的2倍,下列说法正确的是( )
| A. | 质子运动的速率是α粒子的$\sqrt{2}$倍 | |
| B. | 质子与α粒子做圆周运动的周期相等 | |
| C. | 质子与α粒子做圆周运动的半径相等 | |
| D. | 质子所受的洛伦兹力是α粒子的2倍 |
 如图所示,在平面直角坐标系xOy的第四象限有垂直纸面向里的匀强磁场,磁感应强度B=2.0T,一质量为m=5.0×10-8kg、电量为q=1.0×10-6C的带电粒子从P点沿图示方向进入磁场,速度与y轴负方向成θ=37°角,已知OP=30cm,(粒子重力不计,sin37°=0.6,cos37°=0.8),求:
如图所示,在平面直角坐标系xOy的第四象限有垂直纸面向里的匀强磁场,磁感应强度B=2.0T,一质量为m=5.0×10-8kg、电量为q=1.0×10-6C的带电粒子从P点沿图示方向进入磁场,速度与y轴负方向成θ=37°角,已知OP=30cm,(粒子重力不计,sin37°=0.6,cos37°=0.8),求: