题目内容
18. 如图所示,正方型容器处在垂直纸面向里匀强磁场中,一束电子从a孔沿ab射入容器中,其中一部分从c小孔射出,另一部分从d小孔射出,求:
如图所示,正方型容器处在垂直纸面向里匀强磁场中,一束电子从a孔沿ab射入容器中,其中一部分从c小孔射出,另一部分从d小孔射出,求:(1)电子从c、d两孔射入时的速率之比?
(2)从c、d两孔射出的电子在容器中运动所用时间之比?
(3)从c、d两孔射出的电子在容器中运动的加速度大小之比?
分析 (1)电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出粒子的速度,然后求出速度之比.
(2)根据粒子的周期公式与转过的圆心角,然后求出所用时间之比.
(3)由牛顿第二定律求出加速度,然后求出加速度之比.
解答 解:设磁场边长为a,如图所示,粒子从c点离开,其半径为rc,粒子从d点离开,其半径为rd;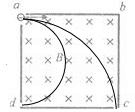
(1)由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{mv}{qB}$,
由运动轨迹可知:rc=2rd
则有:vc:vd=2:1;
(2)粒子周期:T=$\frac{2πm}{qB}$,根据圆心角求出运行时间:t=$\frac{θ}{2π}$T.
运行时间:td=$\frac{1}{2}$T,tc=$\frac{1}{4}$T,则:tc:td=1:2.
(3)加速度为:a=$\frac{{v}^{2}}{r}$,
解得:ac:ad=2:1;
答:(1)电子从c、d两孔射入时的速率之比为2:1;
(2)从c、d两孔射出的电子在容器中运动所用时间之比为:1:2;
(3)从c、d两孔射出的电子在容器中运动的加速度大小之比为:2:1.
点评 本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.掌握带电粒子在匀强磁场中做匀速圆周运动的半径公式r=$\frac{mv}{qB}$,和周期公式T=$\frac{2πm}{qB}$.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
9. 如图所示,A、B是两个完全相同的灯泡,D是理想二极管,L是带铁芯的线圈,其电阻忽略不计.下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,D是理想二极管,L是带铁芯的线圈,其电阻忽略不计.下列说法正确的是( )
 如图所示,A、B是两个完全相同的灯泡,D是理想二极管,L是带铁芯的线圈,其电阻忽略不计.下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,D是理想二极管,L是带铁芯的线圈,其电阻忽略不计.下列说法正确的是( )| A. | S闭合瞬间,A先亮 | |
| B. | S闭合瞬间,A、B同时亮 | |
| C. | S断开瞬间,B逐渐熄灭 | |
| D. | S断开瞬间,A闪亮一下,然后逐渐熄灭 |
13.在磁感应强度为B的匀强磁场中做匀速圆周运动的带电粒子,当磁感应强度突然增大为2B时,这个带电粒子( )
| A. | 速率加倍,周期减半 | B. | 速率不变,轨道半径减半 | ||
| C. | 速率不变,频率减半 | D. | 速率减半,轨道半径不变 |
10.铺设钢轨时,每两根钢轨接缝处都必须留有一定的间隙.每当列车经过轨道接缝处时,车轮就会受到一次冲击.由于每一根钢轨长度相等,所以这个冲击力是周期性的,列车受到周期性的冲击做受迫振动.普通钢轨的长度为12.6m,列车振动的固有频率为3Hz.当列车的行驶速度为25.2m/s时,列车振动的频率为( )
| A. | 2Hz | B. | 3Hz | C. | 1Hz | D. | 0.5Hz |
7.从地面竖直上抛一物体,上升过程先后经过A、B两点,它两次经过A点的时间间隔为tA,两次经过B点的时间间隔为tB,不计空气阻力,则AB相距( )
| A. | $\frac{g}{8}$(tA2-tB2) | B. | $\frac{g}{4}$(tA2-tB2) | C. | $\frac{g}{2}$(tA2-tB2) | D. | g(tA2-tB2) |
 如图所示,电源电动势E=20V,内阻r=1Ω,R1=3Ω,R2=6Ω,C=60μF.
如图所示,电源电动势E=20V,内阻r=1Ω,R1=3Ω,R2=6Ω,C=60μF. 如图所示,为多用表在测量时指针在刻度盘上停留的位置,若选择旋钮在:
如图所示,为多用表在测量时指针在刻度盘上停留的位置,若选择旋钮在: 有一金属细棒ab,质量m=0.05kg,电阻不计,可在两条轨道上滑动,如图所示,轨道间距为L=0.5m,其平面与水平面的夹角为θ=37°,置于垂直于轨道平面向上的匀强磁场中,磁感应强度为B=1.0T,金属棒与轨道的动摩擦因数μ=0.5,(设最大静摩擦力与滑动摩擦力大小相等)回路中电源电动势为E=3V,内阻r=0.5Ω.求:
有一金属细棒ab,质量m=0.05kg,电阻不计,可在两条轨道上滑动,如图所示,轨道间距为L=0.5m,其平面与水平面的夹角为θ=37°,置于垂直于轨道平面向上的匀强磁场中,磁感应强度为B=1.0T,金属棒与轨道的动摩擦因数μ=0.5,(设最大静摩擦力与滑动摩擦力大小相等)回路中电源电动势为E=3V,内阻r=0.5Ω.求: