题目内容
7.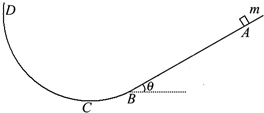 如图所示,倾角θ=37°的斜面与光滑圆弧$\widehat{BCD}$相切于B点,整个装置固定在竖直平面内.有一质量m=2.0kg可视为质点的物体,从斜面上的A处静止下滑,AB长L=3.0m,物体与斜面间的动摩擦因数μ=0.5.不计空气阻力,取重力加速度g=10m/s2、sin37°=0.6、cos37°=0.8.求:
如图所示,倾角θ=37°的斜面与光滑圆弧$\widehat{BCD}$相切于B点,整个装置固定在竖直平面内.有一质量m=2.0kg可视为质点的物体,从斜面上的A处静止下滑,AB长L=3.0m,物体与斜面间的动摩擦因数μ=0.5.不计空气阻力,取重力加速度g=10m/s2、sin37°=0.6、cos37°=0.8.求:(1)物体第一次从A点到B点过程克服摩擦力做功;
(2)物体第一次回到斜面的最高位置距A点距离;
(3)物体在斜面运动的总路程.
分析 (1)应用功的计算公式可以求出克服摩擦力做功.
(2)由动能定理可以求出物体第一次回到斜面的最高位置距A点距离.
(3)应用动能定理可以求出物体的总路程.
解答 解:(1)物体第一次从A点到B点过程克服摩擦力做功:
Wf=μmgLcosθ=0.5×2×10×3×cos37°=24J;
(2)设最高位置距A点距离为x,据动能定理有:
mgxsinθ-μmg(2L-x)cosθ=0,
代入数据解得:解得:x=2.4m;
(3)对整个运动过程,由动能定理得:
mgLsinθ-μmgs总cosθ=0,
代入数据解得:s总=4.5m;
答:(1)物体第一次从A点到B点过程克服摩擦力做功为24J;
(2)物体第一次回到斜面的最高位置距A点距离为2.4m;
(3)物体在斜面运动的总路程为4.5m.
点评 本题考查求功、距离与路程问题,分析清楚物体运动过程,应用动能定理即可正确解题.

练习册系列答案
相关题目
18.有一人造地球卫星的轨道半径是地球半径的n倍,下列说法中正确的是( )
| A. | 该卫星运行速度是第一宇宙速度的$\frac{1}{n}$倍 | |
| B. | 该卫星的运行速度是地球赤道上物体随地球自转获得的速度的$\frac{1}{n}$倍 | |
| C. | 该卫星运行速度是第一宇宙速度$\sqrt{\frac{1}{n}}$倍 | |
| D. | 该卫星的向心加速度是地球表面重力加速度的$\frac{1}{{n}^{2}}$倍 |
15.一辆汽车沿平直公路以速度V1行驶了$\frac{2}{3}$的路程,接着又以速度V2=20Km/h行驶其余的路程,如果汽车对全程的平均速度为28Km/h.那么汽车在前$\frac{2}{3}$路程上速度V1的大小是( )
| A. | 25km/h | B. | 34km/h | C. | 38km/h | D. | 35km/h |
2.质量为2×103kg、发动机额定功率为80kW的汽车在平直公路上行驶,若汽车所受阻力大小恒为4×103N,下列判断正确的是( )
| A. | 汽车行驶能达到的最大速度是40m/s | |
| B. | 汽车从静止开始加速到20m/s的过程,发动机所做功为4×105J | |
| C. | 汽车保持额定功率启动,当速度大小为20m/s时,其加速度大小为6m/s2 | |
| D. | 汽车以2m/s2的恒定加速度启动,发动机在第2秒末的实际功率是32kW |
12. 图中的虚线a、b、c、d表示匀强电场中的4个等势面.两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.已知M是带负电的带电粒子.则下列说法中正确的是( )
图中的虚线a、b、c、d表示匀强电场中的4个等势面.两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.已知M是带负电的带电粒子.则下列说法中正确的是( )
 图中的虚线a、b、c、d表示匀强电场中的4个等势面.两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.已知M是带负电的带电粒子.则下列说法中正确的是( )
图中的虚线a、b、c、d表示匀强电场中的4个等势面.两个带电粒子M、N(重力忽略不计)以平行于等势面的初速度射入电场,运动轨迹分别如图中MPN和NQM所示.已知M是带负电的带电粒子.则下列说法中正确的是( )| A. | N一定也带负电 | B. | a点的电势高于b点的电势 | ||
| C. | 带电粒子N的动能减小电势能增大 | D. | 带电粒子N的动能增大电势能减小 |
19. 一粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的有( )
一粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的有( )
 一粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的有( )
一粒子从A点射入电场,从B点射出,电场的等势面和粒子的运动轨迹如图所示,图中左侧前三个等势面彼此平行,不计粒子的重力.下列说法正确的有( )| A. | 粒子带正电荷 | B. | 粒子的加速度先不变,后变小 | ||
| C. | 粒子的速度不断增大 | D. | 粒子的电势能先减小,后增大 |
16. 如图是质谱仪的原理图,若速度相同的同一束粒子沿极板P1、P2的轴线射入电磁场区域,由小孔S0射入右边的偏转磁场B2中,运动轨迹如图所示,不计粒子重力.下列相关说法中正确的是( )
如图是质谱仪的原理图,若速度相同的同一束粒子沿极板P1、P2的轴线射入电磁场区域,由小孔S0射入右边的偏转磁场B2中,运动轨迹如图所示,不计粒子重力.下列相关说法中正确的是( )
 如图是质谱仪的原理图,若速度相同的同一束粒子沿极板P1、P2的轴线射入电磁场区域,由小孔S0射入右边的偏转磁场B2中,运动轨迹如图所示,不计粒子重力.下列相关说法中正确的是( )
如图是质谱仪的原理图,若速度相同的同一束粒子沿极板P1、P2的轴线射入电磁场区域,由小孔S0射入右边的偏转磁场B2中,运动轨迹如图所示,不计粒子重力.下列相关说法中正确的是( )| A. | 该束带电粒子带负电 | |
| B. | 速度选择器的P1极板带负电 | |
| C. | 在B2磁场中运动半径越大的粒子,质量越大 | |
| D. | 在B2磁场中运动半径越大的粒子,比荷$\frac{q}{m}$越小 |
17. 如图所示,与水平面夹角为30°的固定斜面上有一质量m=1.0kg的物体.细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定于天花板上的弹簧秤相连.物体静止在斜面上,弹簧秤的示数为5.0N.下列说法正确的是(取g=10m/s2)( )
如图所示,与水平面夹角为30°的固定斜面上有一质量m=1.0kg的物体.细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定于天花板上的弹簧秤相连.物体静止在斜面上,弹簧秤的示数为5.0N.下列说法正确的是(取g=10m/s2)( )
 如图所示,与水平面夹角为30°的固定斜面上有一质量m=1.0kg的物体.细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定于天花板上的弹簧秤相连.物体静止在斜面上,弹簧秤的示数为5.0N.下列说法正确的是(取g=10m/s2)( )
如图所示,与水平面夹角为30°的固定斜面上有一质量m=1.0kg的物体.细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定于天花板上的弹簧秤相连.物体静止在斜面上,弹簧秤的示数为5.0N.下列说法正确的是(取g=10m/s2)( )| A. | 斜面对物体的摩擦力大小为零 | |
| B. | 斜面对物体的摩擦力大小为5.0N,方向沿斜面向上 | |
| C. | 斜面对物体的支持力大小为5$\sqrt{3}$N,方向垂直斜面向上 | |
| D. | 斜面对物体的支持力大小为5.0N,方向垂直斜面向上 |
 如图所示,一质量为mA的木块A放在光滑的水平桌面上,A上放置质量为mB的另一木块B,A与B之间的摩擦因数为μ.现施水平力推A,问推力至少为多大时才能使A、B之间发生相对运动.(设最大静摩擦力等于滑动摩擦力)提示:B物体的最大加速度是多大,A物体的加速度不超过B的物体的最大加速度,俩者能否相对滑动.
如图所示,一质量为mA的木块A放在光滑的水平桌面上,A上放置质量为mB的另一木块B,A与B之间的摩擦因数为μ.现施水平力推A,问推力至少为多大时才能使A、B之间发生相对运动.(设最大静摩擦力等于滑动摩擦力)提示:B物体的最大加速度是多大,A物体的加速度不超过B的物体的最大加速度,俩者能否相对滑动.