题目内容
16. 如图所示,质量m=0.5kg的小物块从A点沿竖直光滑的$\frac{1}{4}$圆弧轨道,以vA=2m/s的初速度滑下,圆弧轨道的半径R=0.25m,末端B点与水平传送带相切,物块由B点滑上粗糙的传送带.当传送带静止时,物块滑到传送带的末端C点后做平抛运动,落到水平地面上的D点,已知C点到地面的高度h=5m,C点到D点的水平距离x1=1m,取g=10m/s2.求:
如图所示,质量m=0.5kg的小物块从A点沿竖直光滑的$\frac{1}{4}$圆弧轨道,以vA=2m/s的初速度滑下,圆弧轨道的半径R=0.25m,末端B点与水平传送带相切,物块由B点滑上粗糙的传送带.当传送带静止时,物块滑到传送带的末端C点后做平抛运动,落到水平地面上的D点,已知C点到地面的高度h=5m,C点到D点的水平距离x1=1m,取g=10m/s2.求:(1)物块滑到圆弧轨道底端时对轨道的压力;
(2)物块与传送带之间产生的内能.
分析 (1)从A到B,由动能定理即可求得B点速度,再根据向心力等于轨道对物块支持力与物块重力之差,求出轨道对物块支持力,也就得到了物块滑到圆弧轨道底端时对轨道的压力;
(2)从C到D做平抛运动,可以求出C点的速度,根据从B到C能量守恒,可以求出物块与传送带之间产生的内能.
解答 解:(1)从A到B,由动能定理得:
mgR=$\frac{1}{2}$mvB2-$\frac{1}{2}m{v}_{A}^{2}$
代入数据解得:vB=3m/s
对物块在B点受力分析,由牛顿第二定律可得:
FN-mg=m$\frac{{v}_{B}^{2}}{R}$
代入数据解得:FN=23N
由牛顿第三定律可知:物块滑到圆弧轨道底端时对轨道的压力等于轨道对物块支持力为:FN′=FN=23N;
(2)物块从C运动到D,做平抛运动
则竖直方向:h=$\frac{1}{2}$gt2;
水平方向:x1=vCt
解得:vC=1m/s
物块从B运动到C能量守恒得:
Q=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{C}^{2}$
代入数据解得:Q=2J
答:(1)物块滑到圆弧轨道底端时对轨道的压力是23N;
(2)物块与传送带之间产生的内能是2J.
点评 本题主要考查了动能定理、平抛运动的基本规律,运动学基本公式的应用,要注意传动带顺时针转动时,要分析物体的运动情况,再根据运动学基本公式求解.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
7. 随着国产手机质量的提升,智能手机的市场份额也越来越高,如图所示,是我国某品牌手机的电板,文字说明如图所示.已知该手机充电完成后待机时间为50h,则该电板的电动势和平均待机电流分别为( )
随着国产手机质量的提升,智能手机的市场份额也越来越高,如图所示,是我国某品牌手机的电板,文字说明如图所示.已知该手机充电完成后待机时间为50h,则该电板的电动势和平均待机电流分别为( )
 随着国产手机质量的提升,智能手机的市场份额也越来越高,如图所示,是我国某品牌手机的电板,文字说明如图所示.已知该手机充电完成后待机时间为50h,则该电板的电动势和平均待机电流分别为( )
随着国产手机质量的提升,智能手机的市场份额也越来越高,如图所示,是我国某品牌手机的电板,文字说明如图所示.已知该手机充电完成后待机时间为50h,则该电板的电动势和平均待机电流分别为( )| A. | 3.8V,3000mA | B. | 4.35V,3000mA | C. | 3.8V,60mA | D. | 4.35V,60mA |
7.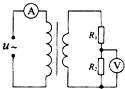 图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
 图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )
图中理想变压器的原、副线圈匝数之比为2:l,电阻R1=R2=10Ω,两电表均为理想交流电表.若R1两端电压瞬时值表达式为u1=10$\sqrt{2}$sin100πt(V),则下列说法正确的是( )| A. | 电流表的示数为0.5A | B. | 电压表示数为14.14V | ||
| C. | R1消耗的功率为20W | D. | 原线圈输入交流电频率为100Hz |
4. 如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
 如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )
如图,两平行金属板AB长L,相距为d,当两板间加上电压U时,质量为m、带电量为q的粒子以速度V0沿两板中线进入,恰好从A极板末端离开电场.当两板间加上一个垂直于纸面的匀强磁场B时,质量为m、带电量为q的粒子同样以速度V0沿两板中线进入,恰好从B极板末端离开该区间.若同时加上U和B,质量为m、带电量为q的粒子以V0沿两板中线进入两板之间,(不计带电粒子的重力)下列说法正确的是( )| A. | 粒子一定带正电 | B. | 粒子一定沿中线运动 | ||
| C. | 粒子一定向着A板偏离中线 | D. | 粒子一定向着B板偏离中线 |
1. 如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
 如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图所示,平行金属板A、B水平正对放置,分别带等量异号电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )| A. | 微粒从M点运动到N点动能一定增加 | |
| B. | 微粒从M点运动到N点电势能一定增加 | |
| C. | 微粒从M点运动到N点机械能可能增加 | |
| D. | 若微粒带正电荷,则A板一定带正电荷 |
13.力F1作用在物体上产生的加速度a1=3m/s2,力F2作用在该物体上产生的加速度a2=4m/s2,则F1和F2同时作用在该物体上,产生的加速度大小不可能为( )
| A. | 8m/s2 | B. | 7m/s2 | C. | 5m/s2 | D. | 1m/s2 |

 要较精确地测量一个量程为0~3V、内阻约3kΩ的电压表V的内阻Rx.除V1外,备用的器材还有:
要较精确地测量一个量程为0~3V、内阻约3kΩ的电压表V的内阻Rx.除V1外,备用的器材还有:
 如图所示,U型细玻璃管竖直放置,各部分水银柱的长度分别为L2=25cm、L3=25cm、L4=10cm,A端被封空气柱的长度为L1=60cm,BC在水平面上.整个装置处在恒温环境中,外界气压P0=75cmHg.将玻璃管绕B点在纸面内沿逆时针方向缓慢旋转90°至AB管水平,求此时被封空气柱的长度.
如图所示,U型细玻璃管竖直放置,各部分水银柱的长度分别为L2=25cm、L3=25cm、L4=10cm,A端被封空气柱的长度为L1=60cm,BC在水平面上.整个装置处在恒温环境中,外界气压P0=75cmHg.将玻璃管绕B点在纸面内沿逆时针方向缓慢旋转90°至AB管水平,求此时被封空气柱的长度.