题目内容
14.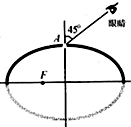 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )| A. | $\frac{4}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
分析 先根据数学知识求出焦点F的坐标,光线从F出发,射到A点,经折射进入该同学的眼中,由几何知识求出入射角i,由折射定律求出的折射率.
解答  解:由椭圆知识可得,焦点F到两轴交点的距离为 c=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2cm,因此光线从F到A时的入射角的正弦为 sinα=$\frac{2}{\sqrt{{2}^{2}+(2\sqrt{3})^{2}}}$=$\frac{1}{2}$,该玻璃的折射率n=$\frac{sin45°}{sinα}$=$\sqrt{2}$.
解:由椭圆知识可得,焦点F到两轴交点的距离为 c=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2cm,因此光线从F到A时的入射角的正弦为 sinα=$\frac{2}{\sqrt{{2}^{2}+(2\sqrt{3})^{2}}}$=$\frac{1}{2}$,该玻璃的折射率n=$\frac{sin45°}{sinα}$=$\sqrt{2}$.
故选:B.
点评 本题涉及的物理知识为光的折射,一要掌握折射定律,二要掌握数学知识:如椭圆的长、短轴和焦点等关系,难度不大.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.设两人造地球卫星的质量比为1:2,到地球球心的距离比为3:1,则它们的( )
| A. | 周期比为27:1 | B. | 线速度比为1:3 | ||
| C. | 向心加速度比为1:9 | D. | 向心力之比为1:9 |
19. 如图所示,a、b是两个带有同种电荷的小球,用绝缘细线悬挂于同一点,两球静止时,它们距水平地面的高度相等,绳与竖直方向的夹角分别为α、β,且α<β.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则( )
如图所示,a、b是两个带有同种电荷的小球,用绝缘细线悬挂于同一点,两球静止时,它们距水平地面的高度相等,绳与竖直方向的夹角分别为α、β,且α<β.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则( )
 如图所示,a、b是两个带有同种电荷的小球,用绝缘细线悬挂于同一点,两球静止时,它们距水平地面的高度相等,绳与竖直方向的夹角分别为α、β,且α<β.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则( )
如图所示,a、b是两个带有同种电荷的小球,用绝缘细线悬挂于同一点,两球静止时,它们距水平地面的高度相等,绳与竖直方向的夹角分别为α、β,且α<β.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则( )| A. | a、b两球同时落地 | B. | a球先落地 | ||
| C. | a球水平飞行的距离比b球大 | D. | a、b两球水平飞行的距离相等 |
6. 如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
 如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )
如图所示为双缝干涉实验中产生的条纹图样,甲图为绿光进行实验的图样,a为中央亮条纹,乙为换用另一种单色光进行实验的图样,a′为中央亮条纹,则以下说法中正确的是( )| A. | 乙图可能是用红光实验产生的条纹,表明红光波长较长 | |
| B. | 乙图可能是用紫光实验产生的条纹,表明紫光波长较长 | |
| C. | 乙图可能是用紫光实验产生的条纹,表明紫光波长较短 | |
| D. | 乙图可能是用红光实验产生的条纹,表明红光波长较短 |
8. 如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
 如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )
如图所示,半圆形的光滑固定轨道槽竖直放置,质量为m的小物体由顶端从静止开始下滑,则物体经过槽底时,对槽底的压力大小为( )| A. | 2mg | B. | 3mg | C. | mg | D. | 5mg |
 图甲所示的平行板电容器板间距离为d,两板所加电压随时间变化图线如图乙所示,t=0时刻,质量为m、带电量为q的粒子以平行于极板的速度v0射入电容器,t1=3T时刻恰好从下极板边缘射出电容器,带电粒子的重力不计,U0、T为已知量,求:
图甲所示的平行板电容器板间距离为d,两板所加电压随时间变化图线如图乙所示,t=0时刻,质量为m、带电量为q的粒子以平行于极板的速度v0射入电容器,t1=3T时刻恰好从下极板边缘射出电容器,带电粒子的重力不计,U0、T为已知量,求: 如图所示:长度L=0.5m的轻质杆OA,A端固定一个质量m=3kg的小球,小球以O为圆心在竖直平面内做圆周运动,小球经过最高点时恰好对杆无压力.(忽略一切阻力,g=10m/s2),求:
如图所示:长度L=0.5m的轻质杆OA,A端固定一个质量m=3kg的小球,小球以O为圆心在竖直平面内做圆周运动,小球经过最高点时恰好对杆无压力.(忽略一切阻力,g=10m/s2),求: