题目内容
4.某行星的一颗卫星围绕行星做匀速圆周运动,其轨道半径为R,运动周期为T,则此行星的质量为$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$.分析 万有引力提供卫星做圆周运动的向心力,由万有引力公式与牛顿第二定律可以求出行星的质量.
解答 解:万有引力提供卫星做圆周运动的向心力,
由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$({\frac{2π}{T})}^{2}$R,
解得,行星的质量:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$;
故答案为:$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$.
点评 本题考查了求行星的质量,要掌握测量天体质量的两种方法;要知道卫星绕行星做圆周运动的向心力是由万有引力提供的,应用万有引力公式与牛顿第二定律可以解题.

练习册系列答案
相关题目
14.下列有关物理学史实的说法中正确的是( )
| A. | 卡文迪许第一个发现了万有引力定律 | |
| B. | 牛顿第一个测出了万有引力常量 | |
| C. | 开普勒第一个发现了行星运动的规律 | |
| D. | 爱因斯坦第一个提出了“日心说” |
15.一个物体做变速运动时,下述说法正确的是( )
| A. | 合外力一定对物体做功,使物体动能发生变化 | |
| B. | 合外力一定对物体做功,但物体的动能可能不变 | |
| C. | 合外力可能不对物体做功,物体动能不变 | |
| D. | 合外力可能对物体做功,使物体动能变化 |
16.用如图甲所示的电路研究光电效应中光电流强度与照射光的强弱、频率等物理量的关系.图中A、K两极间的电压大小可调,电源的正负极也可以对调.分别用a、b、c三束单色光照射,调节A、K间的电压U,得到光电流I与电压U的关系如图乙所示.由图可知( )


| A. | 单色光a和c的频率相同,但a更强些 | |
| B. | 单色光a和c的频率相同,但a更弱些 | |
| C. | 单色光b的频率小于a的频率 | |
| D. | 改变电源的极性不可能有光电流产生 |
14.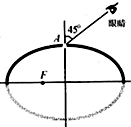 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )| A. | $\frac{4}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
 如图所示,光滑导杆固定在水平地面上,一质量为m的滑块套在导杆上,细绳的一端固定,另一端拴在滑块上,细绳与竖直导杆的夹角为θ.求滑块对细绳的拉力和滑块对导杆的压力.
如图所示,光滑导杆固定在水平地面上,一质量为m的滑块套在导杆上,细绳的一端固定,另一端拴在滑块上,细绳与竖直导杆的夹角为θ.求滑块对细绳的拉力和滑块对导杆的压力.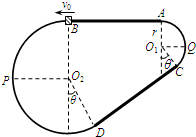 如图是放置在竖直平面内游戏滑轨的模拟装置的示意图.滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD的长度均为L=3m,圆弧形轨道AQC和BPD均光滑,AQC的半径为 r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为=37°.现有一质量为 m=1kg的滑块(可视为质点)穿在滑轨上,以v0=5m/s的初速度从B点开始水平向左运动,滑块与两段直轨道间的动摩擦因数均为μ=0.2,滑块经过轨道连接处的机械能损失忽略不计.取g=10m/s2,sin37°=0.6,求:
如图是放置在竖直平面内游戏滑轨的模拟装置的示意图.滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD的长度均为L=3m,圆弧形轨道AQC和BPD均光滑,AQC的半径为 r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为=37°.现有一质量为 m=1kg的滑块(可视为质点)穿在滑轨上,以v0=5m/s的初速度从B点开始水平向左运动,滑块与两段直轨道间的动摩擦因数均为μ=0.2,滑块经过轨道连接处的机械能损失忽略不计.取g=10m/s2,sin37°=0.6,求: