题目内容
9. 如图所示:长度L=0.5m的轻质杆OA,A端固定一个质量m=3kg的小球,小球以O为圆心在竖直平面内做圆周运动,小球经过最高点时恰好对杆无压力.(忽略一切阻力,g=10m/s2),求:
如图所示:长度L=0.5m的轻质杆OA,A端固定一个质量m=3kg的小球,小球以O为圆心在竖直平面内做圆周运动,小球经过最高点时恰好对杆无压力.(忽略一切阻力,g=10m/s2),求:(1)通过最高点时,小球的速度为多少?
(2)小球到达最低点时,求杆对小球的作用力的大小.
分析 (1)小球经过最高点时恰好对杆无压力,由重力提供向心力,根据牛顿第二定律列式求解;
(2)小球从最高点运动到最低点的过程中,根据动能定理列式,小球在最低点时,根据牛顿第二定律列式,联立方程即可求解.
解答 解:(1)当杆对小球没有作用力时,小球受到的重力作为向心力
$mg=m\frac{{{v}_{1}}^{2}}{L}$
解得${v}_{1}=\sqrt{gL}=\sqrt{5}m/s$
(2)小球从最高点运动到最低点的过程中$\frac{1}{2}m{{v}_{1}}^{2}+2mgL=\frac{1}{2}m{{v}_{2}}^{2}$
小球在最低点时,$F-mg=\frac{m{{v}_{2}}^{2}}{L}$
解得:F=180N
答:(1)通过最高点时,小球的速度为$\sqrt{5}m/s$;
(2)小球到达最低点时,杆对小球的作用力的大小为180N.
点评 本题主要考查了牛顿第二定律及动能定理的直接应用,要求同学们能正确对小球进行受力分析,知道小球经过最高点时恰好对杆无压力,由重力提供向心力,难度不大,属于基础题.

练习册系列答案
相关题目
20.对于光的衍射的定性分析,下列说法中正确的是( )
| A. | 只有障碍物或孔的尺寸可以跟光波波长相比甚至比光的波长还要小的时候,才能明显地产生光的衍射现象 | |
| B. | 光的衍射现象是光波相互叠加的结果 | |
| C. | 光的衍射现象否定了光的直线传播的结论 | |
| D. | 光的衍射现象说明了光具有波动性 |
17.下列关于做匀速圆周运动的物体所受的向心力的说法中,正确的是( )
| A. | 物体除其他的力外还要受到一个向心力 | |
| B. | 物体所受的合外力提供向心力 | |
| C. | 向心力是一个恒力 | |
| D. | 向心力是根据力的性质命名的力 |
4.小船要渡过一条宽d=100m的河,已知小船在静水中的速度为v1=5m/s,河水水流速度为v2=3m/s,则小船以最短距离过河时,所用的时间为( )
| A. | 40s | B. | 44 s | C. | 20s | D. | 25 s |
14.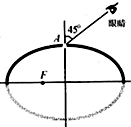 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
 有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )
有一只匀质椭球形玻璃球,长轴为8cm,短轴为4$\sqrt{3}$cm.在椭球的焦点F处有一小气泡,为了测定该玻璃椭球的折射率,某同学将球的上半部表面涂黑,只在球顶A处留出一小块可以透光的地方,如图所示.从A处去看气泡,当视线与短轴的夹角为450时恰好看到气泡,则该玻璃的折射率为( )| A. | $\frac{4}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
1.如图甲所示的变压器为理想变压器,原线圈的匝数n1与副线圈的匝数年n2之比为10:1.变压器的原线圈接如图乙所示的正弦式电流,两个阻值均为R=11Ω的定值电阻串联接在副线圈两端.两个交流电压表均为理想电表.则下列说法不正确的是( )


| A. | 通过两个定值电阻R的交变电流的频率为50Hz | |
| B. | 当t=1×10-2时,电压表V1示数为零 | |
| C. | 当t=1.5×10-2s时,电压表V2示数为11V | |
| D. | 原线圈的输入功率为22W |
18.在水平面上转弯的摩托车,如图所示,提供向心力是( )


| A. | 重力和支持力的合力 | B. | 静摩擦力 | ||
| C. | 滑动摩擦力 | D. | 重力、支持力、牵引力的合力 |
3. 如图所示,一带电液滴(重力不能忽略)在水平向左的匀强电场中,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论正确的是( )
如图所示,一带电液滴(重力不能忽略)在水平向左的匀强电场中,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论正确的是( )
 如图所示,一带电液滴(重力不能忽略)在水平向左的匀强电场中,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论正确的是( )
如图所示,一带电液滴(重力不能忽略)在水平向左的匀强电场中,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论正确的是( )| A. | 此液滴带正电 | B. | 液滴做匀加速直线运动 | ||
| C. | 合外力对液滴做的总功等于零 | D. | 液滴的电势能减少 |
 如图所示,光滑导杆固定在水平地面上,一质量为m的滑块套在导杆上,细绳的一端固定,另一端拴在滑块上,细绳与竖直导杆的夹角为θ.求滑块对细绳的拉力和滑块对导杆的压力.
如图所示,光滑导杆固定在水平地面上,一质量为m的滑块套在导杆上,细绳的一端固定,另一端拴在滑块上,细绳与竖直导杆的夹角为θ.求滑块对细绳的拉力和滑块对导杆的压力.