题目内容
19.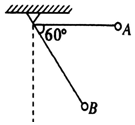 如图所示,一个平行纸面方向未知的匀强电场中,有一上端固定、长为L的绝缘细线,细线下端栓一质量为m、电荷量为+q的小球,开始时将细线拉至水平的A点,释放小球后,球刚好静止在A位置,重力加速度为g,则:
如图所示,一个平行纸面方向未知的匀强电场中,有一上端固定、长为L的绝缘细线,细线下端栓一质量为m、电荷量为+q的小球,开始时将细线拉至水平的A点,释放小球后,球刚好静止在A位置,重力加速度为g,则:(1)若电场方向为竖直方向,求电场强度的大小和方向;
(2)现将小球拉至B点,小球恰好静止在B位置,则所加电场强度的最小值是多大,方向如何?
分析 (1)对小球受力分析,根据共点力平衡求出电场强度的大小和方向.
(2)抓住小球受重力、拉力和电场力处于平衡,结合平行四边形定则求出电场力的最小值,从而得出电场强度的最小值.
解答 解:(1)在A点,小球受重力和电场力处于平衡,有:mg=qE,
解得:E=$\frac{mg}{q}$.
方向:竖直向上.
(2)小球在B点受力如图,当电场力与拉力垂直,电场力最小,
有:mgsin30°=qE′,
解得:$E′=\frac{mg}{2q}$,
电场强度的方向与竖直方向的夹角为60°,指向右上方.
答:(1)电场强度的大小为$\frac{mg}{q}$,方向竖直向上.
(2)所加电场强度的最小值是$\frac{mg}{2q}$,方向与竖直方向的夹角为60°,指向右上方.
点评 本题考查了共点力平衡的基本运用,关键能够正确地受力分析,运用共点力平衡进行求解,会通过平行四边形定则确定力的最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.如图,物体A静止在斜面B上.下列说法正确的是( )


| A. | 斜面B对物块A的弹力方向是竖直向上的 | |
| B. | 斜面B对物块A的弹力方向是垂直斜面向上的 | |
| C. | 物块A受到的弹力是因为物块A发生了形变 | |
| D. | 物块A对斜面B的弹力方向跟物块A恢复形变的方向是相同的 |
14. 如图所示为一水平导轨,A、B为弹性竖直挡板,相距L=8m.小球自A板处开始,以v0=8m/s的速度沿导轨向B运动.它与A、B挡板碰撞后均以与碰前大小相等的速率反弹回来,且在导轨上做减速运动的加速度大小不变.为使小球停在AB的中点,这个加速度的大小可能为( )
如图所示为一水平导轨,A、B为弹性竖直挡板,相距L=8m.小球自A板处开始,以v0=8m/s的速度沿导轨向B运动.它与A、B挡板碰撞后均以与碰前大小相等的速率反弹回来,且在导轨上做减速运动的加速度大小不变.为使小球停在AB的中点,这个加速度的大小可能为( )
 如图所示为一水平导轨,A、B为弹性竖直挡板,相距L=8m.小球自A板处开始,以v0=8m/s的速度沿导轨向B运动.它与A、B挡板碰撞后均以与碰前大小相等的速率反弹回来,且在导轨上做减速运动的加速度大小不变.为使小球停在AB的中点,这个加速度的大小可能为( )
如图所示为一水平导轨,A、B为弹性竖直挡板,相距L=8m.小球自A板处开始,以v0=8m/s的速度沿导轨向B运动.它与A、B挡板碰撞后均以与碰前大小相等的速率反弹回来,且在导轨上做减速运动的加速度大小不变.为使小球停在AB的中点,这个加速度的大小可能为( )| A. | $\frac{1}{3}$m/s2 | B. | 1.5m/s2 | C. | $\frac{8}{3}$m/s2 | D. | 8m/s2 |
8.两个点电荷甲和乙同处于真空中,若把每个电荷的电量都增加为原来的2倍,它们之间的距离保持不变,那么它们之间的相互作用力变为原来的( )
| A. | 4倍 | B. | 2倍 | C. | 8倍 | D. | 1/4 |
 如图所示,在长为L的轻杆中点A和端点B各固定一质量为m的球,杆可绕无摩擦的轴O转动,使杆从水平位置无初速度释放摆下.求,
如图所示,在长为L的轻杆中点A和端点B各固定一质量为m的球,杆可绕无摩擦的轴O转动,使杆从水平位置无初速度释放摆下.求, 如图所示,一质量为m的物体放在竖直的弹簧上,并令其上下作简谐运动.振动过程中物体对弹簧的最大压力为1.7mg,则求
如图所示,一质量为m的物体放在竖直的弹簧上,并令其上下作简谐运动.振动过程中物体对弹簧的最大压力为1.7mg,则求  “探究力的平行四边形定则”的实验如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细线的结点,OB和OC为细绳.图乙所示是在白纸上根据实验结果画出的图.
“探究力的平行四边形定则”的实验如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细线的结点,OB和OC为细绳.图乙所示是在白纸上根据实验结果画出的图.