题目内容
11.弹性势能:Ep=$\frac{1}{2}$kx2.分析 明确弹力表达式并求出前进l时的平均作用力,再用功的公式可求得推力的功;根据功能关系即可明确弹簧的弹性势能的增加量
解答 解:弹力F=kx
力与位移成正比,恒力做功的公式W=FL;
运动l过程中,平均力为:F=$\frac{kx}{2}$;
则平均力做功W=Fl=$\frac{kx}{2}•x$=$\frac{1}{2}$kx2;
因推力做功转化为弹簧的弹性势能;
故弹性势能为:Ep=$\frac{1}{2}$kx2;
故答案为:$\frac{1}{2}$kx2;
点评 弹性势能的表达式课本中并没有直接给出,所以本题考查弹性势能的推导,要注意正确利用平均力来推导,因力是随位移均匀增大的,故平均力为$\frac{F}{2}$.

练习册系列答案
相关题目
1.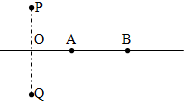 如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
 如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )
如图所示,P、Q是两个电量相等的正的点电荷,它们连线的中点是O,A、B是中垂线上的两点,OA<AB用EA、EB、φA、φB分别表示A、B两点的场强与电势,则( )| A. | EA一定大于EB,φA一定大于φB | B. | EA不一定大于EB,φA一定大于φB | ||
| C. | EA一定大于EB,φA不一定大于φB | D. | EA不一定大于EB,φA不一定大于φB |
6.“嫦娥三号”在环月轨道成功实施变轨控制,从100km×100km的环月圆轨道,降低到近月点15km、远月点100km的椭圆轨道,进入预定的月面着陆准备轨道,并于12月14日21时11分实现卫星携带探测器在月球的软着陆.下列说法正确的是( )
| A. | 如果不考虑地球大气层的阻力,则“嫦娥三号”的发射速度可以小于7.9km/s | |
| B. | 若已知“嫦娥三号”、“嫦娥一号”各自绕月球做匀速圆周运动的高度(高度不同)、周期和万有引力常量,则可求出月球的质量、半径 | |
| C. | 若已知“嫦娥三号”在100km的环月圆轨道上飞行的周期及万有引力常量,则可求出月球的平均密度 | |
| D. | “嫦娥三号”为着陆准备而实施变轨控制时,需要通过发动机使其减速 |
16.三个力分别为10N、20N和30N,则这三个力的合力可能为( )
| A. | 39N | B. | 49N | C. | 59N | D. | 69N |
3.以下的计时数据指时间的是( )
| A. | 上海开往北京的620次列车于13时35分从上海发车 | |
| B. | 某人用13s跑完100m | |
| C. | 中央电视台新闻联播节目19时开播 | |
| D. | 某场足球赛开赛15min时甲队攻入一球 |
20. 如图所示,光滑水平面上,在拉力F作用下,A、B共同以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,A、B质量分别为m1、m2则( )
如图所示,光滑水平面上,在拉力F作用下,A、B共同以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,A、B质量分别为m1、m2则( )
 如图所示,光滑水平面上,在拉力F作用下,A、B共同以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,A、B质量分别为m1、m2则( )
如图所示,光滑水平面上,在拉力F作用下,A、B共同以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,A、B质量分别为m1、m2则( )| A. | a1=0,a2=0 | B. | a1=a,a2=0 | ||
| C. | a1=$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$a,a2=$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$a | D. | a1=a,a2=-$\frac{{m}_{1}}{{m}_{2}}$a |
1. 如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P向上端滑动时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )
如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P向上端滑动时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )
 如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P向上端滑动时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )
如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P向上端滑动时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )| A. | 小灯泡L1变亮,L2、L3变暗 | B. | 小灯泡L3变亮,L1、L2变暗 | ||
| C. | △U1<△U2 | D. | △U1>△U2 |
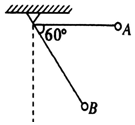 如图所示,一个平行纸面方向未知的匀强电场中,有一上端固定、长为L的绝缘细线,细线下端栓一质量为m、电荷量为+q的小球,开始时将细线拉至水平的A点,释放小球后,球刚好静止在A位置,重力加速度为g,则:
如图所示,一个平行纸面方向未知的匀强电场中,有一上端固定、长为L的绝缘细线,细线下端栓一质量为m、电荷量为+q的小球,开始时将细线拉至水平的A点,释放小球后,球刚好静止在A位置,重力加速度为g,则: