题目内容
7.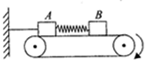 如图所示,两个质量分别为m1、m2的物块A和B通过一轻弹簧连接在一起并放置于水平传送带上,水平轻绳一端连接A,另一端固定在墙上,A、B与传送带间动摩擦因数均为μ.传送带顺时针方向转动,系统达到稳定后,突然剪断轻绳的瞬间,设A、B的加速度大小分别为aA和aB,(弹簧在弹性限度内,重力加速度为g)则( )
如图所示,两个质量分别为m1、m2的物块A和B通过一轻弹簧连接在一起并放置于水平传送带上,水平轻绳一端连接A,另一端固定在墙上,A、B与传送带间动摩擦因数均为μ.传送带顺时针方向转动,系统达到稳定后,突然剪断轻绳的瞬间,设A、B的加速度大小分别为aA和aB,(弹簧在弹性限度内,重力加速度为g)则( )| A. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=μg | B. | aA=μg,aB=0 | ||
| C. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=0 | D. | aA=μg,aB=μg |
分析 分别对物块B和整体分析,通过共点力平衡,结合胡克定律求出两根弹簧的形变量和绳子的拉力;然后结合突然剪断轻绳的瞬间,绳子的拉力减小为0,而弹簧的弹力不变,再分别由牛顿第二定律求出加速度即可.
解答 解:对物块B分析,摩擦力与弹簧弹力平衡,有:μm2g=kx,
则:x=$\frac{μ{m}_{2}g}{k}$.
以两个物块组成的整体为研究对象,则绳子的拉力:T=μ(m1+m2)g
突然剪断轻绳的瞬间,绳子的拉力减小为0,而弹簧的弹力不变,则A受到的合外力与T大小相等,方向相反,则:
aA=$\frac{T}{{m}_{1}}=\frac{μ({m}_{1}+{m}_{2})g}{{m}_{1}}$
B在水平方向仍然受到弹簧的拉力和传送带的摩擦力,合外力不变,仍然等于0,所以B的加速度仍然等于0.故选项C正确,ABD错误.
故选:C
点评 解决本题的关键能够正确地选择研究对象,根据共点力平衡、胡克定律以及牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
相关题目
2.在水平的足够长的固定木板上,一小物块以某一初速度开始滑动,经时间t1后物块停止运动.现将该木板倾斜30°,让小物块以相同大小的初速度沿木板上滑,小物块上滑到最高位置用时t2,则小物块与木板间的动摩擦因数为( )
| A. | $\frac{{t}_{2}}{2{t}_{1}+\sqrt{3}{t}_{2}}$ | B. | $\frac{2{t}_{1}-\sqrt{3}{t}_{2}}{{t}_{1}}$ | C. | $\frac{{t}_{2}}{2{t}_{1}-\sqrt{3}{t}_{2}}$ | D. | $\frac{2{t}_{1}-\sqrt{3}{t}_{2}}{2{t}_{1}}$ |
17.一只“220V 110W”的灯泡接在u=311sin314t(V)的交变电源上,则下列判断错误的是( )
| A. | 在1 min内,灯泡上产生的热量是6600J | |
| B. | 与灯泡串联的电流表的示数为0.5A | |
| C. | 与灯泡并联的电压表的示数为311V | |
| D. | 通过灯泡的电流的表达式为i=0.5sin 314t(A) |
 如图表示某物体的v-t图象,从图象可知
如图表示某物体的v-t图象,从图象可知 打点计时器是高中物理中重要的实验仪器,下图中甲、乙两种打点计时器是高中物理实验中常用的,请回答下列问题:
打点计时器是高中物理中重要的实验仪器,下图中甲、乙两种打点计时器是高中物理实验中常用的,请回答下列问题: 如图1所示,一个圆形线圈的匝数n=1000匝,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间的变化规律如图2所示.求
如图1所示,一个圆形线圈的匝数n=1000匝,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间的变化规律如图2所示.求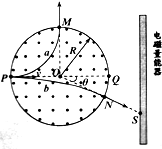 阿尔法磁谱仪(简称AMS)是一个安装于国际空间站上的粒子物理试验设备.假设在某次探测中,观测到从磁场边界的左端点P沿直径PQ垂直磁场方向射入磁场的宇宙射线中含有a和b两种粒子,经磁场偏转后,a、b分别从磁场边界M、N两点离开磁场区域,b与电磁量能器的撞击点为S,如图所示.已知a、b的入射速度大小分别为v1、v2,图形磁场半径为R,O为圆心,磁场方向垂直纸面向外,磁感应强度大小B,OM⊥PQ,∠QON=θ,不考虑粒子间相互作用和相对论效应.
阿尔法磁谱仪(简称AMS)是一个安装于国际空间站上的粒子物理试验设备.假设在某次探测中,观测到从磁场边界的左端点P沿直径PQ垂直磁场方向射入磁场的宇宙射线中含有a和b两种粒子,经磁场偏转后,a、b分别从磁场边界M、N两点离开磁场区域,b与电磁量能器的撞击点为S,如图所示.已知a、b的入射速度大小分别为v1、v2,图形磁场半径为R,O为圆心,磁场方向垂直纸面向外,磁感应强度大小B,OM⊥PQ,∠QON=θ,不考虑粒子间相互作用和相对论效应. 如图所示,光滑管道AB部分平直,BC部分为竖直半圆环,圆环半径为R=10m,现有一个质量为m=2kg半径为r(r<R)的小球,以水平速度v0从管口A端射入管道.小球通过最高点C点时,小球对轨道的压力大小为10N,求小球落回水平管道AB上距离B点多远?(取g=10m/s2)
如图所示,光滑管道AB部分平直,BC部分为竖直半圆环,圆环半径为R=10m,现有一个质量为m=2kg半径为r(r<R)的小球,以水平速度v0从管口A端射入管道.小球通过最高点C点时,小球对轨道的压力大小为10N,求小球落回水平管道AB上距离B点多远?(取g=10m/s2)