题目内容
19.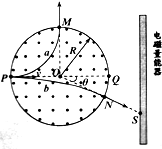 阿尔法磁谱仪(简称AMS)是一个安装于国际空间站上的粒子物理试验设备.假设在某次探测中,观测到从磁场边界的左端点P沿直径PQ垂直磁场方向射入磁场的宇宙射线中含有a和b两种粒子,经磁场偏转后,a、b分别从磁场边界M、N两点离开磁场区域,b与电磁量能器的撞击点为S,如图所示.已知a、b的入射速度大小分别为v1、v2,图形磁场半径为R,O为圆心,磁场方向垂直纸面向外,磁感应强度大小B,OM⊥PQ,∠QON=θ,不考虑粒子间相互作用和相对论效应.
阿尔法磁谱仪(简称AMS)是一个安装于国际空间站上的粒子物理试验设备.假设在某次探测中,观测到从磁场边界的左端点P沿直径PQ垂直磁场方向射入磁场的宇宙射线中含有a和b两种粒子,经磁场偏转后,a、b分别从磁场边界M、N两点离开磁场区域,b与电磁量能器的撞击点为S,如图所示.已知a、b的入射速度大小分别为v1、v2,图形磁场半径为R,O为圆心,磁场方向垂直纸面向外,磁感应强度大小B,OM⊥PQ,∠QON=θ,不考虑粒子间相互作用和相对论效应.(1)判断粒子a的电性,并求出其在磁场中运动的时间;
(2)求粒子b的荷质比$\frac{q}{m}$;
(3)若电磁量能器测得粒子b撞击时的能量为E,b所带电量为多少?
分析 (1)由左手定则从a粒子的偏转方向就能判断a粒子的电性.由于从M点射出,粒子偏转90°,时间为四分之一周期.
(2)由b粒子的偏转角和几何关系求出b粒子做匀速圆周运动的半径,再由洛仑兹力提供向心力就能求得b粒子的比荷.
(3)电磁量能器测得粒子b撞击时的能量为E,该能量为b粒子的动能.由动能公式和前面已经求得的比荷,从而就能求出粒子的电荷量.
解答 解:(1)根据左手定则,粒子a带负电,粒子a从P点进入至M点离开磁场的过程中,偏转了90°角,设运动时间为t,则有:
t=$\frac{1}{4}$T
粒子做圆周运动的周期$T=\frac{2π{r}_{a}}{{v}_{1}}$
由几何关系,粒子a在磁场中做圆周运动的半径ra=R
联立方程得:t=$\frac{πR}{2{v}_{1}}$
(2)由几何关系得,粒子b在磁场中做圆周运动的半径
${r}_{b}=\frac{R}{tan\frac{θ}{2}}$
洛伦兹力提供向心力:qvB=m$\frac{v2}{r}$
即:r=$\frac{mv}{qB}$
所以,粒子b的荷质比
$\frac{q}{m}=\frac{{v}_{2}tan\frac{θ}{2}}{BR}$
(3)粒子b撞击电磁量能器的能量E为粒子的动能,即:
$E=\frac{1}{2}m{{v}_{2}}^{2}$
所以粒子b的质量为:$m=\frac{2E}{{{v}_{2}}^{2}}$
由(2)结论可得,粒子b所带电量为:
$q=\frac{2Etan\frac{θ}{2}}{BR{v}_{2}}$
答:(1)粒子a的电性是带负电,其在磁场中运动的时间为$\frac{πR}{2{v}_{1}}$.
(2)粒子b的荷质比为$\frac{{v}_{2}tan\frac{θ}{2}}{BR}$.
(3)若电磁量能器测得粒子b撞击时的能量为E,b所带电量为$\frac{2Etan\frac{θ}{2}}{BR{v}_{2}}$.
点评 本题涉及阿尔法磁谱仪的工作过程,想象中有两个粒子以相同的能量进入该仪器.分别打在不同位置,根据题设来探测粒子的电性和粒子的比荷.该类问题属简单的带电粒子在圆形磁场区域内做匀速圆周运动问题,由几何关系和牛顿第二定律可以解决问题.

| A. | 一定沿电场线运动 | B. | 一定由高电势处向低电势处运动 | ||
| C. | 不一定沿电场线运动 | D. | 不一定由高电势处向低电势处运动 |
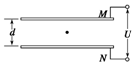 如图所示,平行板电容器两极板M、N相距d,两极板分别与电压恒定为U的电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,则( )
如图所示,平行板电容器两极板M、N相距d,两极板分别与电压恒定为U的电源两极连接,极板M带正电.现有一质量为m的带电油滴在极板中央处于静止状态,则( )| A. | 油滴带负电 | |
| B. | 油滴带正电 | |
| C. | 油滴带电荷量为$\frac{mgd}{U}$ | |
| D. | 将极板N向下缓慢移动一小段距离,油滴将向上运动 |
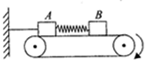 如图所示,两个质量分别为m1、m2的物块A和B通过一轻弹簧连接在一起并放置于水平传送带上,水平轻绳一端连接A,另一端固定在墙上,A、B与传送带间动摩擦因数均为μ.传送带顺时针方向转动,系统达到稳定后,突然剪断轻绳的瞬间,设A、B的加速度大小分别为aA和aB,(弹簧在弹性限度内,重力加速度为g)则( )
如图所示,两个质量分别为m1、m2的物块A和B通过一轻弹簧连接在一起并放置于水平传送带上,水平轻绳一端连接A,另一端固定在墙上,A、B与传送带间动摩擦因数均为μ.传送带顺时针方向转动,系统达到稳定后,突然剪断轻绳的瞬间,设A、B的加速度大小分别为aA和aB,(弹簧在弹性限度内,重力加速度为g)则( )| A. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=μg | B. | aA=μg,aB=0 | ||
| C. | aA=μ(1+$\frac{{m}_{2}}{{m}_{1}}$)g,aB=0 | D. | aA=μg,aB=μg |
 如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=110匝,交流电源的电压u=220$\sqrt{2}$sin100πtV,电压表、电流表均为理想电表,单刀双掷开关开始接a,则以下说法正确的是( )
如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=110匝,交流电源的电压u=220$\sqrt{2}$sin100πtV,电压表、电流表均为理想电表,单刀双掷开关开始接a,则以下说法正确的是( )| A. | 交流电的频率为50Hz | |
| B. | 电压表的示数为22$\sqrt{2}$V | |
| C. | 当开关由a拨至b时,电流表示数变小 | |
| D. | 当开关由a拨至b时,穿过副线圈的磁通量变化率变大 |
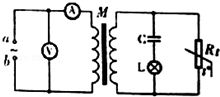 某一火警报警系统原理图如图所示,报警器未画出,a、b接在电压u=311sin314t(V)的正弦交流电源上,Rt为半导体热敏材料制成的传感器,Rt的电阻值随温度升高而减小,下列说法正确的是( )
某一火警报警系统原理图如图所示,报警器未画出,a、b接在电压u=311sin314t(V)的正弦交流电源上,Rt为半导体热敏材料制成的传感器,Rt的电阻值随温度升高而减小,下列说法正确的是( )| A. | 电压表V的示数为220V | |
| B. | 电容器C电容增大,灯L变暗 | |
| C. | Rt所在处出现火警时,电流表A的示数增大 | |
| D. | Rt所在处出现火警时,变压器输入功率减小 |
| A. | 交流电的频率 | B. | 磁通量的变化率 | C. | 功率 | D. | 交流电的峰值 |
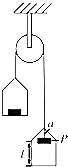 如图所示,轻质滑轮两边分别用细绳悬挂托盘和小重物,每个托盘和小重物的质量均为m,开始托盘和小重物静止,右边小重物P被细绳a悬挂且距离盘底的距离为l,如果某时刻重物P由于细绳a断裂下落,重力加速度为g.
如图所示,轻质滑轮两边分别用细绳悬挂托盘和小重物,每个托盘和小重物的质量均为m,开始托盘和小重物静止,右边小重物P被细绳a悬挂且距离盘底的距离为l,如果某时刻重物P由于细绳a断裂下落,重力加速度为g.