题目内容
3.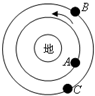 三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )
三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )| A. | 线速度大小:vA>vB=vC | |
| B. | 周期:TA>TB=TC | |
| C. | 向心力大小:FA=FB<FC | |
| D. | 轨道半径和周期的关系:$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
分析 熟悉利用卫星受到的万有引力提供卫星环绕地球运动的向心力列式求解.
解答 解:根据卫星所受万有引力提供向心力有:$G\frac{Mm}{{R}^{2}}=m{a}_{向}=m\frac{{v}^{2}}{R}=m\frac{4{π}^{2}R}{{T}^{2}}$
A、卫星的线速度$v=\sqrt{\frac{GM}{R}}$,得因为RA<RB=RC,所以vA>vB=vC,故A正确;
B、卫星运动行的同期$T=\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$,因为RA<RB=RC,所以TA<TB=TC,故B错误;
C、${F}_{向}=G\frac{Mm}{{R}^{2}}$,RA<RB=RC,mA=mB<mC所以FA>FB,FC>FB,RA<RC,mA<mC故FA和FC大小不确定,故C错误;
D、根据$\frac{{R}^{3}}{{T}^{2}}=\frac{GM}{4{π}^{2}}$,可得$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$,故D正确.
故选:AD.
点评 在卫星运动中,万有引力提供向心力,熟悉掌握万有引力表达式,以及向心力的不同表达式,由万有引力和向心力表达式列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源的内电阻,以下说法中不正确的是( )
如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源的内电阻,以下说法中不正确的是( )
 如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源的内电阻,以下说法中不正确的是( )
如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源的内电阻,以下说法中不正确的是( )| A. | 当R2=R1+r时,R2上获得最大功率 | |
| B. | 当R1=R2+r时,R1上获得最大功率 | |
| C. | 当R2=0时R1上获得功率一定最大 | |
| D. | 当R2=0时,电源的输出功率可能最大 |
11. 两列相干波在介质中叠加,某一时刻如图所示,实线表示波峰,虚线表示波谷.两列波的波长、振幅相同,而且振动步调一致,P、Q、R是叠加区内的三个点,正确说法是( )
两列相干波在介质中叠加,某一时刻如图所示,实线表示波峰,虚线表示波谷.两列波的波长、振幅相同,而且振动步调一致,P、Q、R是叠加区内的三个点,正确说法是( )
 两列相干波在介质中叠加,某一时刻如图所示,实线表示波峰,虚线表示波谷.两列波的波长、振幅相同,而且振动步调一致,P、Q、R是叠加区内的三个点,正确说法是( )
两列相干波在介质中叠加,某一时刻如图所示,实线表示波峰,虚线表示波谷.两列波的波长、振幅相同,而且振动步调一致,P、Q、R是叠加区内的三个点,正确说法是( )| A. | 若二振源振动步调相反,P仍是振动加强点 | |
| B. | R此刻是振动减弱点,过$\frac{3T}{2}$后是振动加强点 | |
| C. | Q点的合位移总是零 | |
| D. | 在叠加区内此刻合位移为零的点也可能是振动加强点 |
8.从同一高度以不同的水平初速度同时抛出两个质量不同的石子,下面说法正确的是( )
| A. | 两石子同时着地 | B. | 质量大的先着地 | ||
| C. | 初速度大的先着地 | D. | 初速度小的先着地 |
13.质量为m的物体沿倾角为θ固定的斜面匀速滑下,在通过位移s的过程中( )
| A. | 重力对物体做功mgssinθ? | |
| B. | 摩擦力对物体做正功,数值为mgssinθ? | |
| C. | 支持力对物体做功mgscosθ? | |
| D. | 合力对物体做功为0 |
 A、B两物体的质量分别为3kg与9kg,相互作用后沿同一直线运动,它们的位移-时间图象如图所示,则A物体在相互作用前后的动量变化是-9
A、B两物体的质量分别为3kg与9kg,相互作用后沿同一直线运动,它们的位移-时间图象如图所示,则A物体在相互作用前后的动量变化是-9 “嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3.
“嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3. 在“研究平抛物体的运动”实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了如图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出,取g=10m/s2.那么小球平抛的初速度为1.5m/s,小球抛出点的坐标为(-30cm,-20cm)(坐标的单位用cm表示).
在“研究平抛物体的运动”实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了如图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出,取g=10m/s2.那么小球平抛的初速度为1.5m/s,小球抛出点的坐标为(-30cm,-20cm)(坐标的单位用cm表示).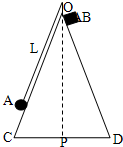 如图所示,有一个光滑的圆锥体固定在水平面上,在其顶点系一根长为L的细线,另一端拴一小物体A,使它刚好能贴着圆锥面做匀速圆周运动(即圆锥体对A无作用力),当运动到图中位置时,从圆锥的顶点O自由释放另一小物体B,使它沿着跟OC对称的另一条母线OD下滑.若圆锥体母线与轴线(OP)间夹角为θ,(设细线不干扰物体B的运动)求:
如图所示,有一个光滑的圆锥体固定在水平面上,在其顶点系一根长为L的细线,另一端拴一小物体A,使它刚好能贴着圆锥面做匀速圆周运动(即圆锥体对A无作用力),当运动到图中位置时,从圆锥的顶点O自由释放另一小物体B,使它沿着跟OC对称的另一条母线OD下滑.若圆锥体母线与轴线(OP)间夹角为θ,(设细线不干扰物体B的运动)求: