题目内容
3.如图1一条东西方向的平直公路边上有两块路牌A、B,A在西,B在东,一辆匀速行驶的汽车自东向西经过路牌B时,一只小鸟恰自A路牌向B匀速飞去,小鸟飞到汽车正上方立即折返,以原速率飞回A,过一段时间后,汽车也行驶到A.以A为OX轴的坐标原点,以向东为x轴正方向,它们的坐标一时间图象如图2所示,图中t2=2t1,由图可知( )
| A. | 小鸟的速率是汽车速率的2倍 | |
| B. | 相遇时小鸟与汽车位移的大小之比是3:1 | |
| C. | 小鸟飞行的总路程是汽车的1.5倍 | |
| D. | 小鸟和汽车在0~t2时间内位移相等 |
分析 本题初看感觉很难,主要原因同学们似乎很难找到解题的突破口,但只要仔细一考虑便不难发现,小鸟飞向B的时间和飞回的时间相同均为$\frac{1}{2}$t1,故有v1$\frac{{t}_{1}}{2}$+v2$\frac{{t}_{1}}{2}$=L,而对于汽车来说有x2=v2t2,再根据t2=2t1,便可轻松解决本题.
解答 解:AB、设AB之间的距离为L,小鸟的速率是v1,汽车的速率是v2,
小鸟从出发到与汽车相遇的时间与汽车返回的时间相同,
故它们相向运动的时间为$\frac{1}{2}$t1,
则在小鸟和汽车相向运动的过程中有:v1•$\frac{1}{2}$t1+v2$\frac{{t}_{1}}{2}$=L,
即:(v1+v2)$\frac{1}{2}$t1=L
对于汽车来说有:v2t2=L
联立以上两式可得:v1=3V2
所以相遇时的位移之比为:3:1;故A错误,B正确;
C、汽车通过的总路程为:x2=v2t2
小鸟飞行的总路程为:x1=v1t1=3V2×$\frac{1}{2}$t2=$\frac{3}{2}$x2,故C正确.
D、小鸟回到出发点,故小鸟的位移为0,而汽车的位移不为零,故D错误.
故选:BC.
点评 能否通过画过程草图,找出两个物体的位移关系、时间关系和速度关系是解决相遇问题的突破口.这一点一定要慢慢领会和使用.也可利用图象法求解.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
11. 如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
 如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )| A. | 电场强度方向由A指向B | B. | 电场强度方向由C指向D | ||
| C. | 粒子到达B点时动能最大 | D. | 粒子到达D点时电势能最小 |
18.关于电场线的说法,正确的是( )
| A. | 电场线的切线方向都和该处正电荷受电场力方向一致 | |
| B. | 正电荷只在电场力作用下一定沿电场线运动 | |
| C. | 沿电场线方向电场强度一定越来越小 | |
| D. | 正电荷沿电场线方向移动其电势能越来越大 |
8.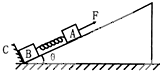 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )| A. | 拉力F做功的等于A动能的增加量 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
12. 如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,斜面体与墙不接触,整个系统处于静止状态.则( )
如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,斜面体与墙不接触,整个系统处于静止状态.则( )
 如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,斜面体与墙不接触,整个系统处于静止状态.则( )
如图所示,质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,轻绳与斜面平行且另一端固定在竖直墙面上,不计小球与斜面间的摩擦,斜面体与墙不接触,整个系统处于静止状态.则( )| A. | 斜面体对水平面的压力等于(M+m)g | |
| B. | 水平面对斜面体有向左的摩擦力作用 | |
| C. | 当滑块缓慢向右移动时,斜面对小球的支持力变大 | |
| D. | 当滑块缓慢向右移动时,细线对小球的拉力先变小 |

 如图所示,水平传送带AB长2m,以v=1m/s的速度匀速运动,质量均为4kg的小物体P、Q与绕过定滑轮的轻绳相连,t=0时刻P、在传送带A端以初速度v0=4m/s向右运动,已知P与传送带间动摩擦因数为0.5,P在传动带上运动过程它与定滑轮间的绳始终水平,不计定滑轮质量和摩擦,绳不可伸长且足够长度,最大静摩擦力视为等于滑动摩擦力,取g=10m/s2,求:
如图所示,水平传送带AB长2m,以v=1m/s的速度匀速运动,质量均为4kg的小物体P、Q与绕过定滑轮的轻绳相连,t=0时刻P、在传送带A端以初速度v0=4m/s向右运动,已知P与传送带间动摩擦因数为0.5,P在传动带上运动过程它与定滑轮间的绳始终水平,不计定滑轮质量和摩擦,绳不可伸长且足够长度,最大静摩擦力视为等于滑动摩擦力,取g=10m/s2,求:
