题目内容
12. 如图所示,在MN右侧有一个磁感应强度B=0.50T的匀强磁场.在磁场中的A点有一静止镭核(${\;}_{88}^{236}$Ra),A点距MN的距离OA=1.0m.D为放置在MN边缘的粒子接收器,OD=1.0m.${\;}_{88}^{236}$Ra发生衰变时,放出某粒子x后变为一氡核(${\;}_{86}^{222}$Rn),接收器D恰好接收到了沿垂直于MN方向射来的粒子x.(近似计算时,可认为核的质量等于质量数乘以原子质量u,1u=1.7×10-27kg.元电荷e=1.6×10-19C).(注:本题计算结果都保留二位有效数字)
如图所示,在MN右侧有一个磁感应强度B=0.50T的匀强磁场.在磁场中的A点有一静止镭核(${\;}_{88}^{236}$Ra),A点距MN的距离OA=1.0m.D为放置在MN边缘的粒子接收器,OD=1.0m.${\;}_{88}^{236}$Ra发生衰变时,放出某粒子x后变为一氡核(${\;}_{86}^{222}$Rn),接收器D恰好接收到了沿垂直于MN方向射来的粒子x.(近似计算时,可认为核的质量等于质量数乘以原子质量u,1u=1.7×10-27kg.元电荷e=1.6×10-19C).(注:本题计算结果都保留二位有效数字)(1)写出上述过程中的核衰变方程(要求写出x的具体符号);
(2)根据x在磁场中的运动特征,求出粒子x的速度大小;
(3)若衰变时释放的核能全部转化成生成物的动能,求该衰变过程所释放的核能.
分析 (1)由质数和核电荷数守恒写核反应方程;
(2)镭核衰变放出α粒子和氡核,分别在磁场中做匀速圆周运动,根据结合关系求出α粒子在磁场中做匀速圆周运动的半径,根据半径公式求出速度,求出α粒子的速度,
(3)衰变过程中动量守恒,求出氡核反冲的动能,两者动能之和即为原来静止的镭核衰变时放出的能量.
解答 解:(1)镭核衰变方程为:${\;}_{88}^{226}{R}_{a}^{\;}$→${\;}_{86}^{222}{R}_{n}^{\;}{+}_{2}^{4}{H}_{e}^{\;}$
(2)x粒子即α粒子在磁场中做匀速圆周运动,轨迹圆心在O点,根据几何关系
根据题意可知,α粒子在磁场中做匀速圆周运动的半径r=1.00m,
设α粒子的速度为v,带电量为q,质量为m,
则有:对x粒子在磁场中匀速圆周运动.根据牛顿第二定律,则有:qvB=4m $\frac{{v}_{\;}^{2}}{r}$
所以v=$\frac{qBr}{4m}$=$\frac{1}{4}$×108m/s
(3)镭核衰变过程动量守恒:0=4mv-222mv'
所以v'=$\frac{1}{222}$×108m/s
故衰变过程释放的核能能为:E=$\frac{1}{2}$×4mv2+$\frac{1}{2}×$222mv′2=2×10-12J;
答:(1)衰变方程:${\;}_{88}^{226}{R}_{a}^{\;}$→${\;}_{86}^{222}{R}_{n}^{\;}{+}_{2}^{4}{H}_{e}^{\;}$
(2)α粒子在磁场中做匀速圆周运动,速度为$\frac{1}{4}×1{0}_{\;}^{8}m/s$
(3)该镭核在衰变为氡核和x粒子时释放的能量2×10-12J.
点评 考查如何书写衰变方程,同时粒子在洛伦兹力作用下做匀速圆周运动时,运用牛顿第二定律,注意动量与动能的关系,并掌握动量守恒定律的应用.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案| A. | “天宫一号”离地面的高度比地球同步卫星离地面的高度小 | |
| B. | “天宫一号”的线速度比地球同步卫星的线速度小 | |
| C. | “天宫一号”的向心加速度比地球同步卫星的向心加速度小 | |
| D. | 当宇航员刘洋站立于“天宫一号”内不动时,她受力平衡 |
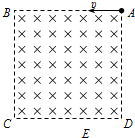 如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )| A. | υ1:υ2:υ3=6:2$\sqrt{3}$:3 | B. | υ1:υ2:υ3=4:3:2 | C. | t1:t2:t3=2:3:4 | D. | t1:t2:t3=3:4:6 |
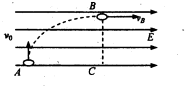 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
 如图所示,电源电动势E=3V,小灯泡L标有“2V、0.4W”,开关S接1,当变阻器调到R=4Ω时,小灯泡L正常发光;现将开关S接2,小灯泡L和电动机M均正常工作,则( )
如图所示,电源电动势E=3V,小灯泡L标有“2V、0.4W”,开关S接1,当变阻器调到R=4Ω时,小灯泡L正常发光;现将开关S接2,小灯泡L和电动机M均正常工作,则( )| A. | 电源内阻为1Ω | B. | 电动机的内阻为4Ω | ||
| C. | 电动机正常工作电压为1V | D. | 电动机消耗的总功率0.16W |
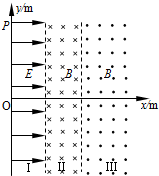 如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:
如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:
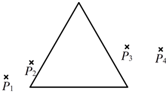 某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.
某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示. 如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.
如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.