题目内容
14.做匀加速直线运动的质点,连续经A、B、C三点,已知AB=BC,且质点在AB段的平均速度为6m/s,在BC段平均速度为12m/s,则下列说法正确的是( )| A. | 通过AB与BC段所用时间之比为1:($\sqrt{2}$-1) | |
| B. | 质点在B点时速度为9m/s | |
| C. | 质点在B点时速度为10m/s | |
| D. | AB段质点速度变化量与BC段速度变化量之比为2:1 |
分析 本题的关键是先设出质点在AB段和BC段运动的时间,然后根据$\overline{v}=\frac{x}{t}$即可求出AC段的平均速度;再由${v}_{\frac{t}{2}}=\frac{x}{t}$结合速度公式即可列式求解.
解答 解:A、根据t=$\frac{x}{t}$可知$\frac{{t}_{1}}{{t}_{2}}=\frac{\frac{x}{{v}_{1}}}{\frac{x}{{v}_{2}}}=\frac{{v}_{2}}{{v}_{1}}=\frac{2}{1}$,故A错误;
B、设质点在AB段运动时间为t1,在BC段运动时间为t2,
由${v}_{\frac{t}{2}}=\frac{x}{t}$可得,AB段中间时刻速度${v}_{\frac{{t}_{1}}{2}}=6m/s$,BC段中间时刻速度${v}_{\frac{{t}_{2}}{2}}=12m/s$,设加速度外a,则B点速度为${v}_{B}={v}_{\frac{{t}_{1}}{2}}+a•\frac{{t}_{1}}{2}$,又${v}_{\frac{{t}_{2}}{2}=}{v}_{B}+a•\frac{{t}_{2}}{2}$,且${t}_{1}=\frac{AB}{6}$,${t}_{2}=\frac{BC}{12}$,
联立以上各式可解得vB=10m/s,aAB=48,所以B错误,C正确,
D、根据△v=a△t可知,AB段质点速度变化量与BC段速度变化量之比为2:1,故D正确
故选:CD
点评 要熟练掌握“在匀变速直线运动中,某段时间内的平均速度等于其中间时刻的瞬时速度”在解题中的灵活应用.

练习册系列答案
相关题目
5.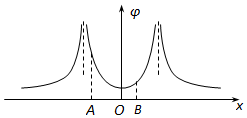 某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )
某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )
 某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )
某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )| A. | φO<φB<φA | B. | EOx<EBx<EAx | C. | EPO<EPB<EPA | D. | EPO-EPA>EPO-EPB |
2.“天宫一号”绕地球的运动可看做匀速圆周运动,转一周所用的时间约90分钟.下列说法正确的是( )
| A. | “天宫一号”离地面的高度比地球同步卫星离地面的高度小 | |
| B. | “天宫一号”的线速度比地球同步卫星的线速度小 | |
| C. | “天宫一号”的向心加速度比地球同步卫星的向心加速度小 | |
| D. | 当宇航员刘洋站立于“天宫一号”内不动时,她受力平衡 |
19. 如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )
如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )
 如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )
如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )| A. | C对B的压力渐减小 | B. | C对B的压力逐渐增大 | ||
| C. | C对B的压力大小不变 | D. | C对B的压力方向不断改变 |
3.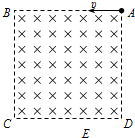 如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
 如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )| A. | υ1:υ2:υ3=6:2$\sqrt{3}$:3 | B. | υ1:υ2:υ3=4:3:2 | C. | t1:t2:t3=2:3:4 | D. | t1:t2:t3=3:4:6 |

 图为某“全家总动员”节目的情景,高台处的水平轨道AB上装有电动悬挂器,水面上有一半径为R=2m的转盘,其轴心在AB正下方,轴心离高台的水平距离为L=5m,高台边缘与转盘平面的高度差为H=5m.选手抓住悬挂器后,在电动机带动下从平台边缘处由静止开始做加速度为a=2m/s2的匀加速直线运动,在某位置松手后落到转盘上.取g=10m/s2.
图为某“全家总动员”节目的情景,高台处的水平轨道AB上装有电动悬挂器,水面上有一半径为R=2m的转盘,其轴心在AB正下方,轴心离高台的水平距离为L=5m,高台边缘与转盘平面的高度差为H=5m.选手抓住悬挂器后,在电动机带动下从平台边缘处由静止开始做加速度为a=2m/s2的匀加速直线运动,在某位置松手后落到转盘上.取g=10m/s2.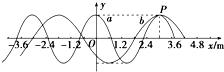 两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.
两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.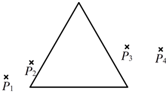 某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.
某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.