题目内容
2.对于在某一轨道绕地球运行的人造地球卫星,若已知其绕地球运行的轨道半径R和周期T(引力常量G为已知),则可求得( )| A. | 该卫星的密度 | B. | 地球的密度 | ||
| C. | 该卫星的向心加速度的大小 | D. | 该卫星所受向心力的大小 |
分析 卫星的万有引力提供向心力,根据牛顿第二定律列式可以求解地球的质量;根据圆周运动的运动学公式可以确定圆周运动的运动参量.
解答 解:A、B、卫星的万有引力提供向心力,故:$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}R$
解得:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
可以求地球的质量,不能求卫星质量;由于不知道地球的体积,无法求解地球的密度;
故A错误,B错误;
C、卫星的向心加速度大小:a=ω2R=$\frac{4{π}^{2}R}{{T}^{2}}$;故C正确;
D、卫星的向心力大小:F=m$\frac{4{π}^{2}R}{{T}^{2}}$;由于不知道卫星的质量,故无法求解卫星的向心力的大小;故D错误;
故选:C.
点评 本题关键是明确卫星的运动学规律和动力学原理,能够结合牛顿第二定律和万有引力定律列式求解,基础题目.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
12.质量相等的甲、乙两颗卫星分别贴近某星球表面和地球表面围绕其做匀速圆周运动,已知该星球和地球的密度相同,半径之比为2:1,则( )
| A. | 甲、乙两颗卫星的加速度之比等于2;1 | |
| B. | 甲、乙两颗卫星所受的向心力之比等于1:1 | |
| C. | 甲、乙两颗卫星的线速度之比等于1:2 | |
| D. | 甲、乙两颗卫星的周期之比等于1:1 |
13.图甲中理想变压器原、副线圈的匝数之比为n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P,下列说法正确的是( )


| A. | 输入电压u的表达式u=20$\sqrt{2}$sin50πtV | |
| B. | 只断开S2后,L1、L2的功率均小于$\frac{P}{4}$ | |
| C. | 只断开S2后,原线圈的输入功率大于$\frac{P}{2}$ | |
| D. | 若S1换接到2后,R消耗的电功率为0.8W |
10. 如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
 如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
17.原子序数大于82的元素的原子核都具有放射性,放射性同位素钍232经一系列衰变会生成氡220.其衰变方程为${\;}_{90}^{232}$Th→${\;}_{86}^{220}$Rn+x${\;}_{4}^{1}$He+y${\;}_{-1}^{0}$e,则其中x和y分别为( )
| A. | 3和2 | B. | 2和3 | C. | 3和3 | D. | 2和2 |
7. 某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )
某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )
 某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )
某导体置于电场后周围的电场分布情况如图所示,图中虚线表示电场线,实线表示等势面.A、B、C为电场中的三个点.下列说法正确的是( )| A. | A点的电场强度大于B点的电场强度 | |
| B. | 将正电荷从A点移到C点,电势能增加 | |
| C. | A点的电势高于B点的电势 | |
| D. | 将负电荷从A点移到B点,电场力做正功 |
14. 如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )
如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )
 如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )
如图所示,一个单匝矩形线圈在有界的匀强磁场中匀速转动,转动轴OO′与磁场方向垂直,线圈abcd关于转动轴对称,线圈的ab边与磁场的边界MN重合,位于图示位置时线圈平面与磁场平行.线圈的面积为S.匀强磁场的磁感应强度为B,线圈转动的角速度为ω.则下列说法中正确的是( )| A. | 若从图示位置开始计时,那么,线圈产生的感应电动势的瞬时值表达式为e=BSωsinωt | |
| B. | 过图示位置时,穿过线圈的磁通量为0.磁通量的变化率为BSω | |
| C. | 经过图示位置时,穿过线圈的磁通量为0.电流的方向发生改变 | |
| D. | 若线圈绕ab轴转动,那么,感应电动势的有效值为$\frac{BSω}{{\sqrt{2}}}$ |
11.一理想变压器原、副线圈的匝数比为44:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
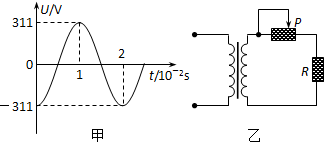

| A. | 副线圈输出电压的频率为100Hz | |
| B. | 副线圈输出电压的有效值为5V | |
| C. | P向左移动时,变压器原、副线圈的电流都减小 | |
| D. | P向左移动时,变压器的输入功率增加 |
