题目内容
17.课外活动小组的同学用图甲所示的实验装置研究小球对轨道的压力与下滑高度的关系.处在竖直平面内的光滑斜面轨道AB与光滑圆弧轨道BCD相切于B点,小球从轨道AB上高H处的某点由静止释放,用与计算机连接的压力传感器测出小球经过圆弧最低点C时对轨道的压力大小FC,不断改变小球的下滑高度H,测出相应的FC,在计算机上作出FC随高度H的变化关系图象,如图乙中图线Ⅰ所示.g=10m/s2.
(1)根据图线Ⅰ,在图乙中作出小球过轨道最高点D时对轨道的压力大小FD随高度H的变化关系图线,并求出小球质量m和圆弧轨道的半径R;
(2)现在D点也安装一个压力传感器,并使轨道CD部分比原来稍粗糙,结果在计算机上得到的FD随高度H的变化关系如图乙中的图线Ⅱ所示.根据图线Ⅰ、Ⅱ,求出小球分别从H1=0.6m、H2=1.2m高度下滑时通过CD段克服摩擦力做的功,并由此分析小球在CD段克服摩擦力做的功Wf与下滑高度H的定性关系.
分析 (1)小球从A到C运动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律和牛顿定律求出小球对轨道C点的压力FC与H的关系式,然后结合F-H图线求出小球质量m和圆弧轨道的半径R.
(2)使轨道CD部分比原来稍粗糙,根据动能定理和牛顿第二定律结合求克服摩擦力做功,再得出Wf与下滑高度H的定性关系.
解答  解:(1)对小球从A运动到C的过程,由动能定理得:
解:(1)对小球从A运动到C的过程,由动能定理得:
mgH=$\frac{1}{2}m{v}_{C}^{2}$
在C点,根据牛顿第二定律得
FC-mg=m$\frac{{v}_{C}^{2}}{R}$
联立解得 FC=$\frac{2mg}{R}$H+mg.
由图乙可知,H=0时,FC=1N,代入上式解得 m=0.1kg
当H=1.2m时,FC=13N,代入上式解得 R=0.2m
对小球从A运动到D的过程,由动能定理得:
mg(H-2R)=$\frac{1}{2}m{v}_{C}^{2}$
在D点,根据牛顿第二定律得
FD+mg=m$\frac{{v}_{D}^{2}}{R}$
联立解得 FD=$\frac{2mg}{R}$H-5mg=$\frac{2×0.1×10}{0.2}$H-5=10H-5(N)
作出FD-H图线如图Ⅲ所示.
(2)由图乙知,当H1=0.6m时,FC=7N,FD=0
在C点,根据牛顿第二定律得
FC-mg=m$\frac{{v}_{C}^{2}}{R}$
在D点,根据牛顿第二定律得
FD+mg=m$\frac{{v}_{D}^{2}}{R}$
根据功能关系可知,小球通过CD段克服摩擦力做的功 Wf1=$\frac{1}{2}m{v}_{C}^{2}$-($\frac{1}{2}m{v}_{D}^{2}$+2mgR)
联立解得 Wf1=0.1J
由图乙知,当H2=1.2m时,FC=13N,FD=5N,运用同样的方法可得 Wf2=0.2J
可知,小球下滑高度越高,克服摩擦力做的功越多
答:
(1)如图Ⅲ所示.小球质量m和圆弧轨道的半径R分别为0.1 kg和0.2 m.
(2)小球分别从H1=0.6m、H2=1.2m高度下滑时通过CD段克服摩擦力做的功分别为0.1J和0.2 J,小球下滑高度越高,克服摩擦力做的功越多.
点评 本题通过动能定理和牛顿第二定律求出F与H的表达式是解决本题的关键,列出解析式,再作图象是常用的方法,要学会应用.

 阅读快车系列答案
阅读快车系列答案
| A. | 变压器可以改变交变电压但不能改变频率 | |
| B. | 扼流圈对交流的阻碍作用是因为线圈存在电阻 | |
| C. | 真空冶炼炉的工作原理是炉体产生涡流使炉内金属熔化 | |
| D. | 磁电式仪表中用来做线圈骨架的铝框能起电磁阻尼的作用 |
 如图为两列简谐横波t=0时刻的波形图,a沿x轴正方向传播,b沿x轴负方向传播,波速都是10m/s.下列说法正确的是( )
如图为两列简谐横波t=0时刻的波形图,a沿x轴正方向传播,b沿x轴负方向传播,波速都是10m/s.下列说法正确的是( )| A. | 横波a的周期为0.4s | |
| B. | x=2m处质点的振幅为1cm | |
| C. | t=0时,x=1m处质点的位移为-1cm | |
| D. | t=0时,x=1m处的质点向y轴负方向振动 | |
| E. | t=2.3s时,x=2m处的质点位移为-3cm |
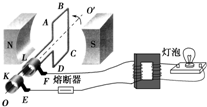 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈线接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈线接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )| A. | 变压器原、副线圈匝数之比为25:11 | |
| B. | 线框中产生交变电压的有效值为500$\sqrt{2}$V | |
| C. | 图示位置穿过线框的磁通量为零 | |
| D. | 允许变压器输出的最大功率为5000W |
 如图,一列简谐横波沿x轴正方向传播,波幅A=2cm,周期T=1.2×10-2s.t=0时,相距50cm的两质点a、b的位移都是$\sqrt{3}$cm,但振动方向相反,其中a沿y轴负方向运动.下列说法正确的是( )
如图,一列简谐横波沿x轴正方向传播,波幅A=2cm,周期T=1.2×10-2s.t=0时,相距50cm的两质点a、b的位移都是$\sqrt{3}$cm,但振动方向相反,其中a沿y轴负方向运动.下列说法正确的是( )| A. | t=2×10-2时质点a第一次回到平衡位置 | |
| B. | 当质点b的位移为+2cm时,质点a的位移为-2cm | |
| C. | 质点a和质点b的速度在某一时刻可能相同 | |
| D. | 这列波的波长可能为$\frac{3}{7}$m | |
| E. | 这列波的波速可能为0.6m/s |
 如图所示,平行线代表电场线,带电量为+10-6C的带电粒子,只受电场力作用,当它从A点运动到B点时(轨迹为虚线1、2中的某一条)动能减少了10-5J,已知A点的电势为-10V,则以下判断正确的是( )
如图所示,平行线代表电场线,带电量为+10-6C的带电粒子,只受电场力作用,当它从A点运动到B点时(轨迹为虚线1、2中的某一条)动能减少了10-5J,已知A点的电势为-10V,则以下判断正确的是( )| A. | B点电势为-20V,粒子运行规矩可能是1 | |
| B. | B点电势为0V,粒子运行规矩可能是1 | |
| C. | B点电势为0V,粒子运行规矩可能是2 | |
| D. | B点电势为-20V,粒子运行规矩可能是2 |
 如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )
如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )| A. | 物块在A点的电势能EPA=+Qφ | |
| B. | 物块在A点时受到轨道的支持力大小为mg+$\frac{3\sqrt{3}kQq}{{8h}^{2}}$ | |
| C. | 点电荷+Q产生的电场在B点的电场强度大小EB=k$\frac{Q}{{h}^{2}}$ | |
| D. | 点电荷+Q产生的电场在B点的电势φB=$\frac{m({{v}_{0}}^{2}-{v}^{2})}{2q}$+φ |
 一理想变压器原,副线圈的匝数比为n1:n2=10:1,原线圈通过理想电流表A接在u=200$\sqrt{2}$sinl00πr(v)的正弦交流电源上,电路如图所示,则( )
一理想变压器原,副线圈的匝数比为n1:n2=10:1,原线圈通过理想电流表A接在u=200$\sqrt{2}$sinl00πr(v)的正弦交流电源上,电路如图所示,则( )| A. | 电压表的读数为20$\sqrt{2}$V | |
| B. | 滑动变阻器的滑片向上滑动时,变压器的输入功率变小 | |
| C. | 滑动变阻器的滑片向下滑动时,电流表的读数变小 | |
| D. | 滑动变阻器的滑片向下滑动时,电压表的读数变小 |
