题目内容
13. 如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )
如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )| A. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| B. | 从A到B的过程中,电场力对点电荷乙做的功为W=μmgL+$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 | |
| C. | 从A到B的过程中,电场力对点电荷乙做的功为W=μmgL+$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | |
| D. | 从A到B的过程中,电势能的减少量小于克服摩擦力做的功 |
分析 本题首先要正确分析物体受力特点,明确力和运动的关系,在本题中注意滑动摩擦力的大小方向不变,两球靠近过程中库仑力逐渐增大,小球先减速后加速,根据牛顿第二定律和功能关系可正确解答.
解答 解:A、由题意,乙到达B点时速度最小,乙先减速运动后做加速运动,当速度最小时有:mgμ=F库=k$\frac{Qq}{{r}^{2}}$,解得r=$\sqrt{\frac{kQq}{μmg}}$,故A正确;
B、C从A到B的过程中,根据动能定理得:W-μmgL=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$,得W=μmgL+$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$,故B错误,C正确.
D、根据以上分析可知,电场力做功值小于摩擦力做功值,因此电势能的减少量小于克服摩擦力做的功,故D正确.
本题选错误的,故选:B.
点评 本题在借助库仑力的基础知识,考查了力与运动、牛顿第二定理、动能定理等基础知识的综合应用,是考查学生综合能力的好题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
4. 如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
 如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )| A. | 不断增加 | B. | 不断减少 | C. | 先增大后减少 | D. | 先减少后增大 |
8.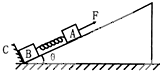 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )| A. | 拉力F做功的等于A动能的增加量 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
18.如图所示是某导体的I-U图象,图中α=45°,下列说法错误的是( )


| A. | 通过电阻的电流与其两端的电压成正比 | |
| B. | 此导体的电阻R=2Ω | |
| C. | I-U图象的斜率为电阻的倒数,所以R=cot45°=1.0Ω | |
| D. | R两端加6.0 V电压时,每秒通过导体截面的电荷量是3.0C |
5.质量为m的物体竖直下落,重力加速度为g.从静止到速度为v的过程中,重力的平均功率为( )
| A. | mv | B. | mgv | C. | $\frac{1}{2}$mv2 | D. | $\frac{1}{2}$mgv |
2.对于库仑定律,下面说法正确的是( )
| A. | 库仑定律适用于真空中两个点电荷之间的相互作用力 | |
| B. | 两个带电小球即使相距非常近,也能用库仑定律 | |
| C. | 相互作用的两个点电荷,不论它们的电荷量是否相同,它们之间的库仑力大小一定相等 | |
| D. | 两个点电荷的电量各减为原来的一半,它们之间的距离保持不变,则它们之间库存仑力减为原来的一半 |
3.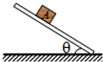 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )| A. | 物块与木板之间的摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| B. | 将木块与水平面的视角改为60°,再释放物块,其运动加速度为$\frac{10\sqrt{3}}{3}$m/s2 | |
| C. | 将木板与水平面的倾角改为60°,再释放物块,其运动到木板下端的速度为2$\sqrt{3}$m/s | |
| D. | 将木板与水平桌面的倾角改为60°,再释放物块,其运动到木板下端的过程中重力做功5$\sqrt{3}$J |