题目内容
3.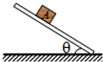 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )| A. | 物块与木板之间的摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| B. | 将木块与水平面的视角改为60°,再释放物块,其运动加速度为$\frac{10\sqrt{3}}{3}$m/s2 | |
| C. | 将木板与水平面的倾角改为60°,再释放物块,其运动到木板下端的速度为2$\sqrt{3}$m/s | |
| D. | 将木板与水平桌面的倾角改为60°,再释放物块,其运动到木板下端的过程中重力做功5$\sqrt{3}$J |
分析 根据物块平衡列方程,可求得物块与木板之间的动摩擦因数;再由动能定理等可求得物块的速度及重力所做的功.
解答 解:A、物块平衡可知mgsinθ=μmgcosθ,物块与木板之间的动摩擦因数μ=tanθ=$\frac{{\sqrt{3}}}{3}$,故A正确;
B、将木板与水平面的倾角改为600,则mgsinθ-μmgcosθ=ma,则物块运动加速度为$\frac{{10\sqrt{3}}}{3}$,故B正确;
C、将木板与水平面的倾角改为600,物块运动到木板下端的速度v2=2ax,则v=2$\sqrt{5}$m/s,故C错误;
D、将木板与水平面的倾角改为600,物块运动到木板下重力做功W=mgh=15J,故D错误
故选:AB
点评 本题考查平衡方程和牛顿第二定律的综合应用,要注意正确受力分析,根据物理过程选择正确的物理规律.

练习册系列答案
相关题目
13. 如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )
如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )
 如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )
如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L.则下列说法错误的是( )| A. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| B. | 从A到B的过程中,电场力对点电荷乙做的功为W=μmgL+$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 | |
| C. | 从A到B的过程中,电场力对点电荷乙做的功为W=μmgL+$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | |
| D. | 从A到B的过程中,电势能的减少量小于克服摩擦力做的功 |
15. 如图为氢原子的四个能级图,现用频率为v的光子使大量处于n=2能级的原子被激发到n=4的能级,这些处于n=4能级的原子将向低能级跃迁,则在跃迁时应有( )
如图为氢原子的四个能级图,现用频率为v的光子使大量处于n=2能级的原子被激发到n=4的能级,这些处于n=4能级的原子将向低能级跃迁,则在跃迁时应有( )
 如图为氢原子的四个能级图,现用频率为v的光子使大量处于n=2能级的原子被激发到n=4的能级,这些处于n=4能级的原子将向低能级跃迁,则在跃迁时应有( )
如图为氢原子的四个能级图,现用频率为v的光子使大量处于n=2能级的原子被激发到n=4的能级,这些处于n=4能级的原子将向低能级跃迁,则在跃迁时应有( )| A. | 可能放出光子,也可能吸收光子 | |
| B. | 只能放出三种频率的光子 | |
| C. | 可能放出6中频率的光子,但最大频率不会大于v | |
| D. | 放出光子的频率有的大于v,但最小频率不会大于v |
13. 如图所示,足够长的光滑斜面中间虚线区域内有一垂直于斜面向上的匀强磁场,一正方形线框从斜面底端以一定初速度上滑,线框越过虚线进入磁场,最后又回到斜面底端,则下列说法中正确的是( )
如图所示,足够长的光滑斜面中间虚线区域内有一垂直于斜面向上的匀强磁场,一正方形线框从斜面底端以一定初速度上滑,线框越过虚线进入磁场,最后又回到斜面底端,则下列说法中正确的是( )
 如图所示,足够长的光滑斜面中间虚线区域内有一垂直于斜面向上的匀强磁场,一正方形线框从斜面底端以一定初速度上滑,线框越过虚线进入磁场,最后又回到斜面底端,则下列说法中正确的是( )
如图所示,足够长的光滑斜面中间虚线区域内有一垂直于斜面向上的匀强磁场,一正方形线框从斜面底端以一定初速度上滑,线框越过虚线进入磁场,最后又回到斜面底端,则下列说法中正确的是( )| A. | 上滑过程线框中产生的焦耳热等于下滑过程线框中产生的焦耳热 | |
| B. | 上滑过程线框中产生的焦耳热大于下滑过程线框中产生的焦耳热 | |
| C. | 上滑过程线框克服重力做功的平均功率等于下滑过程中重力的平均功率 | |
| D. | 上滑过程线框克服重力做功的平均功率大于下滑过程中重力的平均功率 |

 如图所示为甲乙两物体的一次运动的速度-时间图象:
如图所示为甲乙两物体的一次运动的速度-时间图象:
