题目内容
17. 在倾角为30°的光滑斜面底端固定一挡板,质量均为m的物块B、C通过轻弹簧连接,且均处于静止状态,此时弹簧的压缩量为x0,O点为弹簧的原长位置.在斜面上距物块B的距离为3x0的P点由静止释放一质量为m的物块A,A与B相碰(不粘连)后立即一起沿斜面向下运动,并恰好能返回到O点.物块A、B、C均可视为质点,重力加速度为g.
在倾角为30°的光滑斜面底端固定一挡板,质量均为m的物块B、C通过轻弹簧连接,且均处于静止状态,此时弹簧的压缩量为x0,O点为弹簧的原长位置.在斜面上距物块B的距离为3x0的P点由静止释放一质量为m的物块A,A与B相碰(不粘连)后立即一起沿斜面向下运动,并恰好能返回到O点.物块A、B、C均可视为质点,重力加速度为g.(1)求A、B碰前弹簧具有的弹性势能;
(2)若物块A从P点以一定的初速度沿斜面下滑,两物块A、B返回O点时还具有沿斜面向上的速度,此后恰好可以使C离开挡板而不上滑,求物块A在P点的初速度v0.
分析 (1)先研究A下滑过程,根据机械能守恒定律求得A与B碰撞前瞬间的速度.再A、B碰撞过程,由动量守恒定律求得碰后共同速度.最后研究A、B整体从压缩弹簧到运动到O点的过程,对A、B及弹簧构成的系统,运用机械能守恒定律列式,即可求解A、B碰前弹簧具有的弹性势能;
(2)C恰好离开挡板而不上滑时,弹簧的弹力大小等于C的重力沿斜面向下的分力大小,且AB运动到了最高点.与上题思路相似进行解答.
解答 解:(1)A从P下滑3x0过程,由机械能守恒定律得:
mg•3x0sin30°=$\frac{1}{2}m{v}^{2}$
A与B碰撞过程,取沿斜面向下为正方向,根据动量守恒定律得:
mv=2mv′
A、B整体从压缩弹簧到运动到O点的过程,对A、B及弹簧构成的系统,由机械能守恒定律得:
$\frac{1}{2}×2mv{′}^{2}$+Ep=2mgx0sin30°.
联立以上三式解得:A、B碰前弹簧具有的弹性势能为:
Ep=$\frac{1}{4}$mgx0sin30°
(2)A以初速度v0从P下滑3x0过程,由机械能守恒定律得:
mg•3x0sin30°=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
A与B碰撞过程,取沿斜面向下为正方向,根据动量守恒定律得:
2mv2=mv1.
初态时,弹簧的压缩量为:
x1=$\frac{mgsin30°}{k}$=x0
C恰好离开挡板而不上滑时,弹簧的弹力大小等于C的重力沿斜面向下的分力大小,弹簧的伸长量为:
x2=$\frac{mgsin30°}{k}$
所以x1=x2=x0,初、末状态弹簧的弹性势能相等,设为Ep.
A、B整体从压缩弹簧到运动到O点的过程,对A、B及弹簧构成的系统,由机械能守恒定律得:
$\frac{1}{2}×2m{v}_{2}^{2}$+Ep=2mgx0sin30°+$\frac{1}{2}×2m{v}_{3}^{2}$.
对B及弹簧,在B从O点到最高点的过程中,由机械能守恒定律得
$\frac{1}{2}m{v}_{3}^{2}$=mgx0sin30°+Ep.
联立解得:v0=$\sqrt{6g{x}_{0}}$
答:
(1)A、B碰前弹簧具有的弹性势能是$\frac{1}{4}$mgx0sin30°.
(2)物块A在P点的初速度v0是v0$\sqrt{6g{x}_{0}}$.
点评 本题的关键要分析清楚物体的运动过程,把握每个过程的物理规律,如碰撞的基本规律:动量守恒定律.物体压缩弹簧的过程,系统遵守机械能守恒定律,并要找出状态之间的联系.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案| A. | 0 | B. | 8N | C. | 12N | D. | 24N |
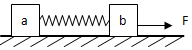 如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )
如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )| A. | 弹簧对a物体的弹力小于对b物体的弹力 | |
| B. | a受到的弹簧的拉力为F-μmbg | |
| C. | b物体在水平方向只受两个力的作用 | |
| D. | a、b之间的距离为L+$\frac{μmag}{k}$ |
 将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )
将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )| A. | A掷出时的初速度一定比B大 | B. | B插入靶时的末速度一定比A大 | ||
| C. | B运动时间一定比A长 | D. | A的质量一定比B大 |
 如图,将一正电荷从电场线上的a点移到b点,电势φa=10V,φb=5V.下列判断正确的是( )
如图,将一正电荷从电场线上的a点移到b点,电势φa=10V,φb=5V.下列判断正确的是( )| A. | 该电场是匀强电场 | B. | a点场强大于b点场强 | ||
| C. | 电场线方向由a指向b | D. | 正电荷的电势能减小 |
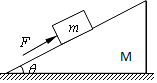 如图所示,质量为m=5kg的物体,置于倾角为θ=30°的粗糙斜面块上,用一平行于斜面的大小为30N的力推物体,使其沿斜面向上匀速运动,g=10m/s2.求:
如图所示,质量为m=5kg的物体,置于倾角为θ=30°的粗糙斜面块上,用一平行于斜面的大小为30N的力推物体,使其沿斜面向上匀速运动,g=10m/s2.求: 一个物体从光滑斜面的顶端由静止开始下滑,斜面长10m,倾角θ=30°,斜面静止不动,物体的质量M=2kg,重力加速度g取10m/s2.求:
一个物体从光滑斜面的顶端由静止开始下滑,斜面长10m,倾角θ=30°,斜面静止不动,物体的质量M=2kg,重力加速度g取10m/s2.求: