题目内容
11.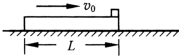 如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求:
如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求:(1)滑块相对于长木板的运动时间;
(2)木板的最小长度.
分析 (1)滑块恰好不从木板上掉下来,滑块滑到木板的左端,且两者速度相等.根据牛顿第二定律求出两者的加速度,再根据速度相等关系由速度公式列式,即可求时间.
(2)由位移时间公式求两者的位移,它们的位移之差即等于木板的最小长度.
解答 解:(1)根据牛顿第二定律得滑块的加速度为:a1=$\frac{μmg}{m}$=μg=2m/s2,
木板的加速度为:${a_2}=\frac{μmg}{M}$=$\frac{0.2×1×10}{4}$=0.5 m/s2.
滑块恰好不从木板上掉下来,满足:$v_0^{\;}-a_1^{\;}t={a_2}t$,
解得:t=4s.
(2)滑块的位移为:x1=$\frac{1}{2}{a}_{1}{t}^{2}$=$\frac{1}{2}×2×{4}^{2}$=16m
木板的位移为:${x_2}={v_0}t-\frac{1}{2}{a_1}{t^2}$=10×4-$\frac{1}{2}$×0.5×42=36m
所以木板的最小长度为:L=x2-x1=20m.
答:(1)滑块相对于长木板的运动时间是4s;
(2)木板的最小长度是20m.
点评 对于滑块在木板上滑动的类型,研究的方法比较多,本题采用牛顿第二定律和运动学公式结合的方法解决,也可以根据动量守恒定律和能量守恒定律结合研究.

练习册系列答案
相关题目
2. 如图甲所示是一台交流发电机的构造示意图,线圈转动产生的感应电动势随时间变化的规律如图乙所示,发电机线圈电阻为1Ω,外接负载电阻为4Ω,则( )
如图甲所示是一台交流发电机的构造示意图,线圈转动产生的感应电动势随时间变化的规律如图乙所示,发电机线圈电阻为1Ω,外接负载电阻为4Ω,则( )
 如图甲所示是一台交流发电机的构造示意图,线圈转动产生的感应电动势随时间变化的规律如图乙所示,发电机线圈电阻为1Ω,外接负载电阻为4Ω,则( )
如图甲所示是一台交流发电机的构造示意图,线圈转动产生的感应电动势随时间变化的规律如图乙所示,发电机线圈电阻为1Ω,外接负载电阻为4Ω,则( )| A. | 线圈转速为50r/s | |
| B. | 电压表的示数为4V | |
| C. | 负载电阻的电功率为2W | |
| D. | 线圈转速加倍,电压表读数变为原来的4倍 |
3.一个质点做匀加速直线运动,在时间间隔t内发生的位移为x,动能变为原来的4倍,该质点运动的加速度大小为( )
| A. | $\frac{2x}{3{t}^{2}}$ | B. | $\frac{2x}{5{t}^{2}}$ | C. | $\frac{2x}{{t}^{2}}$ | D. | $\frac{x}{3{t}^{2}}$ |
20. 利用速度传感器与计算机结合,可以自动做出物体的速度v随时间t的变化图象.某次实验中获得的v-t图象如图所示,由此可以推断该物体在( )
利用速度传感器与计算机结合,可以自动做出物体的速度v随时间t的变化图象.某次实验中获得的v-t图象如图所示,由此可以推断该物体在( )
 利用速度传感器与计算机结合,可以自动做出物体的速度v随时间t的变化图象.某次实验中获得的v-t图象如图所示,由此可以推断该物体在( )
利用速度传感器与计算机结合,可以自动做出物体的速度v随时间t的变化图象.某次实验中获得的v-t图象如图所示,由此可以推断该物体在( )| A. | t=2 s时速度的方向发生了变化 | B. | t=2 s时加速度的方向发生了变化 | ||
| C. | 0~4 s内做曲线运动 | D. | 0~4 s内的位移约为2.8 m |
7.伏安法测电阻的方法有图示的甲、乙两种电路,电压表、电流表均非理想电表,下列说法正确的是( )

| A. | 两种电路接法完全等效 | |
| B. | 按甲电路连法,测得值偏小 | |
| C. | 若待测电阻的阻值很大,用甲电路测量误差较小 | |
| D. | 若待测电阻的阻值很小,用甲电路测量误差较小 |
 长为L质量为M的木板A静止在光滑的水平桌面上,有一质量为m的小木块B以水平速度V0恰好落在木板A的左端,如图所示,木块B与木块A间的摩擦系数为μ,木块B可视为质点,试求:
长为L质量为M的木板A静止在光滑的水平桌面上,有一质量为m的小木块B以水平速度V0恰好落在木板A的左端,如图所示,木块B与木块A间的摩擦系数为μ,木块B可视为质点,试求:

