题目内容
16.如图小球在竖直平面内转动,小球质量为m,转动半径为R,分析下列情况
①轻绳系一小球在竖直平面内做圆周运动,最高点的最小速度是多少;
②轻秆固定一小球在竖直平面内做圆周运动,最高点的最小速度是多少;
③小球沿竖直平面内光滑圆环的内侧做圆周运动,最高点的最小速度多少;
④小球在竖直平面内的光滑管内做圆周运动,最高点的最小速度是多少.
分析 小球在竖直平面内做圆周运动,由于绳子不能支撑小球,在最高点时,拉力最小为零.对于杆,由于杆对小球可以是支持力,故最高点的合力可以为零,结合牛顿第二定律求得速度
解答 解:(1)在最高点当小球只受重力时,速度最小,根据牛顿第二定律可知mg=$\frac{m{v}^{2}}{R}$,解得v=$\sqrt{gR}$
(2)对于杆,可以给小球支持力,当 支持力等于重力时速度最小,则$mg-{F}_{N}=\frac{m{v}^{2}}{R}$,其中FN=mg,解得v=0
(3)球沿竖直平面内光滑圆环的内侧做圆周运动,当圆环对小球的支持力为零时,速度最小,根据牛顿第二定律可知mg=$\frac{m{v}^{2}}{R}$,解得v=$\sqrt{gR}$
(4)小球在竖直平面内的光滑管内做圆周运动,当内环对小球的支持力等于重力时速度最小,则$mg-{F}_{N}=\frac{m{v}^{2}}{R}$,其中FN=mg,解得v=0
答:①轻绳系一小球在竖直平面内做圆周运动,最高点的最小速度是$\sqrt{gR}$
②轻秆固定一小球在竖直平面内做圆周运动,最高点的最小速度是0;
③小球沿竖直平面内光滑圆环的内侧做圆周运动,最高点的最小速度$\sqrt{gR}$;
④小球在竖直平面内的光滑管内做圆周运动,最高点的最小速度是0.
点评 该题考查竖直平面内的圆周运动,对于圆周运动动力学问题,重在分析向心力的来源,利用牛顿第二定律列方程分析.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
1.如图是一个中学物理中常用的力学实验装置,关于此装置,下列说法中正确的有( )


| A. | 用此装置“研究匀变速直线运动”时必须平衡摩擦力 | |
| B. | 用此装置“探究小车的加速度与质量的关系”并用图象法处理数据时,如果画出的α-M关系图象是一条曲线,就可以确定加速度与质量成反比 | |
| C. | 用此装置“探究功与速度变化的关系”时,将木板左端适当垫高,目的是为了平衡摩擦力 | |
| D. | 用此装置“探究小车的加速度与外力的关系”时,若用钩码的重力代替绳子对小车的拉力,应让钩码质量远小于小车质量 |
8.如图甲所示,理想变压器原、副线圈的匝数比n1:n2=10:1,b是原线圈的中心抽头,S为单刀双掷开关,定值电阻R=10Ω,从某时刻开始在原线圈c、d两端加上如图乙所示的交变电压,则下列说法正确的是( )


| A. | 当S与a连接后,t=0.01s时理想电流表示数为零 | |
| B. | 当S与a连接后,理想电压表的示数为22$\sqrt{2}$V | |
| C. | 当S由a拨到b后,原线圈的输入功率变为原来的4倍 | |
| D. | 当S由a拨到b后,副线圈输出电压的频率变为25Hz |
12.下列关于静电学公式的理解,正确的是( )
| A. | F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$只对点电荷成立 | B. | E=k$\frac{q}{{r}^{2}}$只对匀强电场成立 | ||
| C. | E=$\frac{F}{q}$只对点电荷成立 | D. | U=$\frac{W}{q}$只对匀强电场成立 |
 如图所示,若将A、B两个光滑带电小球静止放在无阻力的水平管道内,其中A的质量为M,B的质量为m,(M>m).开始时两球之间相距很远,现在给A一个初速度v,让其向右运动. 已知两球之间由于带同种电荷会相互排斥,选取无穷远为参考面,两带电小球的电势能为$\frac{K}{r}$,其中K 为已知常数,r为两球之间的距离.问:
如图所示,若将A、B两个光滑带电小球静止放在无阻力的水平管道内,其中A的质量为M,B的质量为m,(M>m).开始时两球之间相距很远,现在给A一个初速度v,让其向右运动. 已知两球之间由于带同种电荷会相互排斥,选取无穷远为参考面,两带电小球的电势能为$\frac{K}{r}$,其中K 为已知常数,r为两球之间的距离.问: 如图所示,在光滑的水平面上,有两个质量分别为MA=8kg、MB=10kg的小车A和B,两车之间用轻质弹簧相连,它们以共同的速度v0=3m/s向右匀速运动(弹簧为原长),另有一质量m=2kg的粘性小球C,从距A车上表面竖直高度为h=1.8m的某处以v=8m/s的速度向右水平抛出,正好黏在A车上,不计空气阻力,g=10m/s2,所有计算结果均保留2位有效数字,求:
如图所示,在光滑的水平面上,有两个质量分别为MA=8kg、MB=10kg的小车A和B,两车之间用轻质弹簧相连,它们以共同的速度v0=3m/s向右匀速运动(弹簧为原长),另有一质量m=2kg的粘性小球C,从距A车上表面竖直高度为h=1.8m的某处以v=8m/s的速度向右水平抛出,正好黏在A车上,不计空气阻力,g=10m/s2,所有计算结果均保留2位有效数字,求:
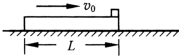 如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求:
如图所示,一木板置于光滑的水平面上,可视为质点的滑块置于木板的右侧,滑块与木板之间的动摩擦因数为μ=0.2.木板的质量为M=4kg,滑块的质量m=1kg.一开始滑块静止,木板以初速度v0=10m/s向右运动,滑块恰好不从木板上掉下来,取g=10m/s2,试求: 某同学在“测量电源的电动势和内阻”的实验中,所需器材如下:
某同学在“测量电源的电动势和内阻”的实验中,所需器材如下: