题目内容
11.如图甲所示,“ ”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图乙所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求:
”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图乙所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求: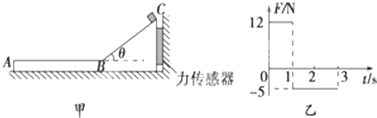
(1)斜面BC的长度;
(2)滑块的质量;
(3)运动过程中滑块克服摩擦力做的功.
分析 (1)当滑块沿斜面BC向下运动时,滑块对斜面有斜向右下方的压力,则力传感器受到压力.由图读出滑块运动的时间为t=1s,由牛顿第二定律求出滑块的加速度,即可由位移公式求解斜面BC的长度.
(2)滑块对斜面的压力为N1′=mgcosθ,木板对传感器的压力为:F1=N1′sinθ,由图读出F1,即可求得滑块的质量.
(3)求出滑块滑到B点的速度,根据牛顿第二定律求出加速度,根据运动学基本公式求出位移,进而求出克服摩擦力所做的功.
解答  解:(1)分析滑块受力,由牛顿第二定律得:
解:(1)分析滑块受力,由牛顿第二定律得:
得:a1=gsinθ=6m/s2
通过图象可知滑块在斜面上运动时间为:t1=1s
由运动学公式得:L=$\frac{1}{2}$a1t12=3m
(2)滑块对斜面的压力为:N1′=mgcosθ
木板对传感器的压力为:F1=N1′sinθ
由图象可知:F1=12N
解得:m=2.5kg
(3)滑块滑到B点的速度为:v1=a1t1=6m/s
由图象可知:f1=5N,t2=2s
a2=$\frac{f}{m}$=2m/s2
s=v1t2-$\frac{1}{2}$a2t22=8m
W=fs=40J
答:(1)斜面BC的长度L为3m;
(2)滑块的质量m为2.5kg;
(3)运动过程中滑块克服摩擦力做的功W为40J.
点评 本题要读懂F-t图象,分析滑块的受力情况和运动情况,关键要抓住木板对传感器的压力与滑块对斜面BC压力的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.水平抛出的小球,t秒末的速度方向与水平方向的夹角为θ1,t+t0秒末速度方向与水平方向的夹角为θ2,忽略空气阻力,重力加速度为g,则小球初速度的大小为( )
| A. | gt0(cos θ1-cos θ2) | B. | $\frac{g{t}_{0}}{cos{θ}_{1}-cos{θ}_{2}}$ | ||
| C. | gt0(tanθ2-tanθ1) | D. | $\frac{g{t}_{0}}{tan{θ}_{2}-tan{θ}_{1}}$ |
16.飞船在地球向上发射后,先绕地球在低轨道上运行,随后变轨到高轨道上运行,经过一段时间后,进行回收返回到地球.以下说法正确的是( )
| A. | 飞船从地面发射时处于超重状态 | |
| B. | 飞船在高轨道运行速度大于在低轨道运行速度 | |
| C. | 飞船从低轨道要经过制动减速才能变轨到高轨道 | |
| D. | 飞船从低轨道变到高轨道机械能保持不变 |


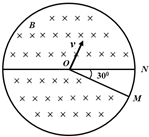 如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力.
如图所示,在圆形区域中圆心角为30°的扇面MON之外分布着垂直于纸面向里的匀强磁场,磁感应强度大小为B,一质量为m、带电量为-q的粒子,自圆心O点垂直于OM以速度v射入磁场,粒子恰能两次经过边界OM,不计粒子重力.
