题目内容
5.A、B两颗卫星围绕地球做匀速圆周运动,A卫星运行的周期为T1,轨道半径为r1;B卫星运行的周期为T2,且T1>T2.下列说法正确的是( )| A. | B卫星的轨道半径为r1($\frac{{T}_{1}}{{T}_{2}}$)${\;}^{\frac{2}{3}}$ | |
| B. | A卫星的机械能一定大于B卫星的机械能 | |
| C. | 某时刻卫星A、B在轨道上相距最近,从该时刻起每经过$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$时间,卫星A、B再次相距最近 | |
| D. | A、B卫星在轨道上运行时处于完全失重状态,不受任何力的作用 |
分析 根据开普勒第三定律求B卫星的轨道半径.由卫星从第轨道进入高轨道需要加速度,由于不知道各自的质量.故不能研究机械能的大小.当卫星转过的圈数相差一圈时两卫星再次最近.由此列式分析.
解答 解:A、根据开普勒第三定律可得$\frac{{r}_{1}^{3}}{{r}_{2}^{3}}$=$\frac{{T}_{1}^{2}}{{T}_{2}^{2}}$,则得B卫星的轨道半径为 r2=r1($\frac{{T}_{2}}{{T}_{1}}$)${\;}^{\frac{2}{3}}$.故A错误.
B、因T1>T2.由上分析知,r1>r2,根据将卫星从低轨道进入高轨道,火箭要点火加速做功,但由于A与B的质量都未知,故无法判定谁的机械能更大.故B错误.
C、设从两卫星相距最近到再次相距最近经历时间为t.则有 2π=$\frac{2π}{{T}_{2}}$t-$\frac{2π}{{T}_{1}}$t,得 t=$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$.故C正确.
D、A、B卫星在轨道上运行时由万有引力提供向心力,处于完全失重状态,但仍受万有引力的作用.故D错误.
故选:C.
点评 卫星类型关键要建立物理模型:卫星绕地球做匀速圆周运动,地球的万有引力提供卫星的向心力,可结合开普勒定律分析.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.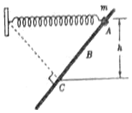 如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
 如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻弹簧一端固定,另一端与质量为m、套在倾斜固定杆A处的圆环相连,弹簧水平.圆环从A处由静止释放,经过杆上B处的速度最大,到达C处的速度为零,在C处时弹簧处于原长且弹簧与斜杆垂直,A、C高度差为h.如果圆环在C处获得一沿斜杆向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 上滑经过B的速度大于下滑经过B的速度 | |
| C. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| D. | 在A处,弹簧的弹性势能为mgh-$\frac{1}{4}$mv2 |
17.物理学家通过实验来探究自然界的物理规律,为人类的科学事业做出了巨大的贡献.下列符合物理史实的是( )
| A. | 法拉第通过精心设计的实验,发现了电磁感应现象,首先发现电与磁存在联系 | |
| B. | 伽利略最先把科学实验和逻辑推理方法相结合,否认了力是维持物体运动状态的原因 | |
| C. | 卡文迪许利用扭秤实验装置测量出了万有引力常量,牛顿在此基础上提出了万有引力定律 | |
| D. | 开普勒用了20年时间观测记录行星的运动,发现了行星运动的三大定律 |
14.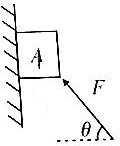 如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
 如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )
如图所示,物体A的质量为m,受到推力F的作用,靠在光滑的竖直墙上,物体保持静止,则下列说法正确的是( )| A. | 物体A受到4个力作用 | B. | mg=Fcosθ | ||
| C. | 物体A对墙的压力为Fcosθ | D. | 撤去F后,物体A做自由落体运动 |
19.物理学史上有很多物理学家做出具大的贡献,以下叙述正确的是( )
| A. | 牛顿发现了万有引力定律并测出了引力常量 | |
| B. | 伽利略通过对物体运动的研究,提出了“力是维持物体运动的原因”这一观点 | |
| C. | 法拉第首先发现了电磁感应现象,使人们能够成功地将机械能转化为电能 | |
| D. | 安培发现了电流能产生磁场,并提出了著名的分子电流假说 |
 如图所示,竖直放置的导热气缸内用活塞封闭着一定质量的理想气体,活塞的质量为m,横截面积为S,缸内气体高度为2h.现在活塞上缓慢添加砂粒,直至缸内气体的高度变为h.然后再对气缸缓慢加热,让活塞恰好回到原来位置.已知大气压强为p0,大气温度均为T0,重力加速度为g,不计活塞与气缸间摩擦.求:
如图所示,竖直放置的导热气缸内用活塞封闭着一定质量的理想气体,活塞的质量为m,横截面积为S,缸内气体高度为2h.现在活塞上缓慢添加砂粒,直至缸内气体的高度变为h.然后再对气缸缓慢加热,让活塞恰好回到原来位置.已知大气压强为p0,大气温度均为T0,重力加速度为g,不计活塞与气缸间摩擦.求: 如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.
如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.