��Ŀ����
4�� ��ͼ��ʾ����ֱƽ������һֱ������ϵ����y����Ҳ����ˮƽ�������ǿ�糡����ǿ��СΪE����y������ͬʱ����һ����ֱֽ�����⡢�Ÿ�Ӧǿ�ȴ�СΪB��ˮƽ����Ϊa����ǿ�ų�����һ���������������硢�Ⱥ�Ϊ$\frac{q}{m}$��������+x����ijһλ�����ٶ��ͷţ�
��ͼ��ʾ����ֱƽ������һֱ������ϵ����y����Ҳ����ˮƽ�������ǿ�糡����ǿ��СΪE����y������ͬʱ����һ����ֱֽ�����⡢�Ÿ�Ӧǿ�ȴ�СΪB��ˮƽ����Ϊa����ǿ�ų�����һ���������������硢�Ⱥ�Ϊ$\frac{q}{m}$��������+x����ijһλ�����ٶ��ͷţ���1������ǡ�þ����ų�����߽���P�㣨-a��$\frac{a}{2}$��������������ų�����ٶ�v1�Ĵ�С��
��2������ǿ�ų������ͬʱ����һ����ֱֽ������Ÿ�Ӧǿ�ȴ�СҲΪB��������ǿ�ų���Ҫʹ���ӵڶ�����+x�����˶�ʱǡ����y���ϵ�M�㣨0��-4a������������+x�������ٶ��ͷ�ʱ��λ�����꣮
���� ��1������ţ�ٵڶ����ɣ������������ṩ����������ϼ��ι�ϵ��������⣻
��2�������˶��켣�����ݼ��ι�ϵ��������֪������뾶�Ĺ�ϵ���ٽ�϶��ܶ�����������⣮
��� �⣺��1����ͼ��ʾ���ɼ��ι�ϵ��֪��${r}_{1}^{2}={a}^{2}+��{r}_{1}-\frac{a}{2}��^{2}$��
��֪�������ڴų����˶��켣�뾶r1=$\frac{5a}{4}$��
��ţ�ٵڶ����ɣ��ɵã�$Bq{v}_{1}=m\frac{{v}_{1}^{2}}{{r}_{1}}$
�������ų����ٶ�v1=$\frac{5Bqa}{4m}$��
��2��Ҫʹ���ӵڶ�����+x�����˶�ʱ��ǡ�þ���y���ϵ�M�㣨0��-4a�����켣��ͼ��ʾ��
����ͼ��֪���ڡ�O1O2D�У�O1O2=2r3��O2D=2a��O1D=r3+a��
�ɼ��ι�ϵ����֪��$��2{r}_{3}��^{2}=��2a��^{2}+��{r}_{3}+a��^{2}$��
��ã�${r}_{3}=\frac{5}{3}a$��
��Bqv3=$\frac{m{v}_{3}^{2}}{{r}_{3}}$��
�����ڵ糡�����ȼ���ֱ���˶������У�qEx=$\frac{1}{2}m{v}_{3}^{2}-0$��
��+x�������ٶ��ͷ�ʱ��λ������x=$\frac{25q{B}^{2}{a}^{2}}{18mE}$��
�𣺣�1����������ų�����ٶ�v1�Ĵ�С$\frac{5Bqa}{4m}$��
��2������+x�������ٶ��ͷ�ʱ��λ������$\frac{25q{B}^{2}{a}^{2}}{18mE}$��
���� ���������ڵ糡�м�����ų���ƫת������ţ�ٵڶ������붯�ܶ����������˶�ѧ����������ʽ��ע�⼸�ι�ϵ����ȷ������

| A�� | $\frac{p}{q}$v | B�� | $\frac{q}{p}$v | C�� | $\sqrt{\frac{p}{q}}$v | D�� | $\sqrt{\frac{q}{p}}$v |
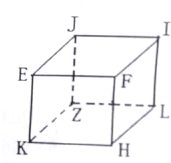 ��ͼ��ʾ����������EFIJKHLZ���ڵĿռ��д���һ����ǿ�糡������E��F��I��Z�ĵ���Ʀ�E=5V����F=8V����I=12V����Z=6V��������˵����ȷ���ǣ�������
��ͼ��ʾ����������EFIJKHLZ���ڵĿռ��д���һ����ǿ�糡������E��F��I��Z�ĵ���Ʀ�E=5V����F=8V����I=12V����Z=6V��������˵����ȷ���ǣ�������| A�� | H��ĵ���Ϊ5V | |
| B�� | �糡ǿ�ȷ���һ����I��K��������ߴ�ֱ | |
| C�� | E��K��������Ʋ���I��L����ĵ��Ʋ���� | |
| D�� | ��2C����ɴ�F���Ƶ�Z�㣬���ۺ���·��������Ҫ�˷��糡������4J |
 ��ͼ��ʾ�����Ϊ�ȵ�б��̶���ˮƽ�����ϣ��䶥����һ�ᵯ�ɣ������϶˹̶���һ����Ϊm��С������һ��в�����б�森��С�����б����͵�A���ٶ�Ϊv��������ѹ�������ʱС���λ��C�㣬C������߶�Ϊh��С�����б���Ķ�Ħ��ϵ��Ϊ�̣�����С����뵯����ײ�����е�������ʧ����С�����C��ʱ���ɵĵ�������Ϊ��������
��ͼ��ʾ�����Ϊ�ȵ�б��̶���ˮƽ�����ϣ��䶥����һ�ᵯ�ɣ������϶˹̶���һ����Ϊm��С������һ��в�����б�森��С�����б����͵�A���ٶ�Ϊv��������ѹ�������ʱС���λ��C�㣬C������߶�Ϊh��С�����б���Ķ�Ħ��ϵ��Ϊ�̣�����С����뵯����ײ�����е�������ʧ����С�����C��ʱ���ɵĵ�������Ϊ��������| A�� | $\frac{1}{2}$mv2-mgh-��mghcot�� | B�� | mgh+$\frac{1}{2}$mv2-mghtan�� | ||
| C�� | $\frac{1}{2}$mv2-mgh | D�� | mgh-$\frac{1}{2}$mv2+��mghcot�� |


 ��ͼ��ʾ��һˮƽ���ʹ���v=6m/s���ٶ�˳ʱ���˶�����ת����M��N֮��ľ���L=10m��һ����m=3kg�����壨����Ϊ�ʵ㣩����ڴ��ʹ�������ߣ�M�ֵ����Ϸ�������֪�����봫�ʹ�֮��Ķ�Ħ��������=0.3����������M�����͵�N���Ĺ����У���
��ͼ��ʾ��һˮƽ���ʹ���v=6m/s���ٶ�˳ʱ���˶�����ת����M��N֮��ľ���L=10m��һ����m=3kg�����壨����Ϊ�ʵ㣩����ڴ��ʹ�������ߣ�M�ֵ����Ϸ�������֪�����봫�ʹ�֮��Ķ�Ħ��������=0.3����������M�����͵�N���Ĺ����У��� ��ͼ����ֹ��A�������ӣ������ٵ糡���ٺ���ͼ��Բ������ͨ���������������P�㴹ֱCN�������������н���ǿ�糡���糡����ˮƽ�����������ͨ�����о��ȷ���ֲ��ĵ糡����֪Բ�����ߵİ뾶ΪR�������ڴ���ǿΪE��������ͼ��ʾ����������Ϊm�������Ϊq��$\overline{QN}$=2d��$\overline{PN}$=3d�������������ƣ�
��ͼ����ֹ��A�������ӣ������ٵ糡���ٺ���ͼ��Բ������ͨ���������������P�㴹ֱCN�������������н���ǿ�糡���糡����ˮƽ�����������ͨ�����о��ȷ���ֲ��ĵ糡����֪Բ�����ߵİ뾶ΪR�������ڴ���ǿΪE��������ͼ��ʾ����������Ϊm�������Ϊq��$\overline{QN}$=2d��$\overline{PN}$=3d�������������ƣ� ��ͼ���������L=0.8m�����費�Ƶ�ƽ�й⻬��������ˮƽ���ã�һ������ֵR=0.3���ĵ�������������x��0һ�������x�������������Ⱥ�ų����䷽���뵼��ƽ�洹ֱ���仯��k=0.5T/m��x=0���ų��ĴŸ�Ӧǿ��B0=0.5T��һ������m=0.2kg������r=0.1���Ľ��������ڵ����ϣ����뵼�촹ֱ���������������´�x=0���Գ��ٶ�v0=8m/s�ص��������˶����˶������е������ĵĹ��ʲ��䣮��
��ͼ���������L=0.8m�����費�Ƶ�ƽ�й⻬��������ˮƽ���ã�һ������ֵR=0.3���ĵ�������������x��0һ�������x�������������Ⱥ�ų����䷽���뵼��ƽ�洹ֱ���仯��k=0.5T/m��x=0���ų��ĴŸ�Ӧǿ��B0=0.5T��һ������m=0.2kg������r=0.1���Ľ��������ڵ����ϣ����뵼�촹ֱ���������������´�x=0���Գ��ٶ�v0=8m/s�ص��������˶����˶������е������ĵĹ��ʲ��䣮��