题目内容
14.某行星的质量为地球质量的p倍,半径为地球半径的q倍,已知地球的第一宇宙速度为v,则该行星的第一宇宙速度为( )| A. | $\frac{p}{q}$v | B. | $\frac{q}{p}$v | C. | $\sqrt{\frac{p}{q}}$v | D. | $\sqrt{\frac{q}{p}}$v |
分析 物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,大小7.9km/s,可根据卫星在圆轨道上运行时的速度公式v=$\sqrt{\frac{GM}{r}}$解得.
解答 解:设地球质量M,某星球质量6M,地球半径r,某星球半径1.5r
由万有引力提供向心力做匀速圆周运动得:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,
解得:卫星在圆轨道上运行时的速度公式v=$\sqrt{\frac{GM}{r}}$
分别代入地球和某星球的各物理量得:v地球=$\sqrt{\frac{GM}{r}}$
v星球=$\sqrt{\frac{G•pM}{qr}}=\sqrt{\frac{p}{q}}v$,故C正确、ABD错误.
故选:C.
点评 本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
4. 如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
 如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )| A. | F1>F2 | B. | F1=F2 | C. | Uab>Ucd | D. | Uab=Ucd |
5.如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100πrad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V,1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )

| A. | 电压表的读数为448V | |
| B. | 输电线路的电流为0.98A | |
| C. | 电流表的读数为2.5A | |
| D. | 降压变压器的原副线圈匝数比为5:1 |
9. 如图所示,挡板垂直于斜面固定在斜面上,一滑块m放在斜面上,其上表面呈弧形且左端最薄,一球M搁在挡板与弧形滑块上,一切摩擦均不计,用平行于斜面的拉力F拉住弧形滑块,使球与滑块均静止.现将滑块平行于斜面向上拉过一较小的距离,球仍搁在挡板与滑块上且处于静止状态,则与原来相比( )
如图所示,挡板垂直于斜面固定在斜面上,一滑块m放在斜面上,其上表面呈弧形且左端最薄,一球M搁在挡板与弧形滑块上,一切摩擦均不计,用平行于斜面的拉力F拉住弧形滑块,使球与滑块均静止.现将滑块平行于斜面向上拉过一较小的距离,球仍搁在挡板与滑块上且处于静止状态,则与原来相比( )
 如图所示,挡板垂直于斜面固定在斜面上,一滑块m放在斜面上,其上表面呈弧形且左端最薄,一球M搁在挡板与弧形滑块上,一切摩擦均不计,用平行于斜面的拉力F拉住弧形滑块,使球与滑块均静止.现将滑块平行于斜面向上拉过一较小的距离,球仍搁在挡板与滑块上且处于静止状态,则与原来相比( )
如图所示,挡板垂直于斜面固定在斜面上,一滑块m放在斜面上,其上表面呈弧形且左端最薄,一球M搁在挡板与弧形滑块上,一切摩擦均不计,用平行于斜面的拉力F拉住弧形滑块,使球与滑块均静止.现将滑块平行于斜面向上拉过一较小的距离,球仍搁在挡板与滑块上且处于静止状态,则与原来相比( )| A. | 滑块对球的弹力增大 | B. | 挡板对球的弹力减小 | ||
| C. | 斜面对滑块的弹力增大 | D. | 拉力F不变 |
6.一定质量的理想气体,如果保持它的体积不变,降低温度,使它的压强变为0℃时压强的$\frac{1}{n}$,则此时气体的摄氏温度数值是( )
| A. | $\frac{-273}{n}$ | B. | $\frac{273(n-1)}{n}$n | C. | $\frac{-273(n-1)}{n}$ | D. | $\frac{273n}{(n-1)}$ |
3. 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )| A. | 若图中霍尔元件是电子导电,则下板电势高 | |
| B. | 磁感应强度B越大,上、下表面的电势差U越小 | |
| C. | 电流I取值越大,上、下表面的电势差U越小 | |
| D. | k越大,传感器灵敏度($\frac{△U}{△z}$)越高 |
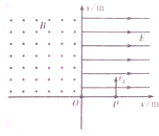 如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球:
如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球: 如图所示,在y>0的空间中存在匀强电场,电场方向沿y轴正方向;在y<0的空间中存在匀强磁场,磁场方向垂直平面(纸面)向里,一电荷量为q、质量为m的带负电的运动粒子,经过y轴上y=h处的点P1时速度大小为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,再经x=-2h的P3点再次进入电场.粒子重力不计.求:
如图所示,在y>0的空间中存在匀强电场,电场方向沿y轴正方向;在y<0的空间中存在匀强磁场,磁场方向垂直平面(纸面)向里,一电荷量为q、质量为m的带负电的运动粒子,经过y轴上y=h处的点P1时速度大小为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,再经x=-2h的P3点再次进入电场.粒子重力不计.求: 如图所示,竖直平面内有一直角坐标系,在y轴的右侧存在水平向左的匀强电场,场强大小为E.在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场Ⅰ.有一不计重力、带正电、比荷为$\frac{q}{m}$的粒子由+x轴上某一位置无初速度释放.
如图所示,竖直平面内有一直角坐标系,在y轴的右侧存在水平向左的匀强电场,场强大小为E.在y轴的左侧同时存在一个垂直纸面向外、磁感应强度大小为B、水平宽度为a的匀强磁场Ⅰ.有一不计重力、带正电、比荷为$\frac{q}{m}$的粒子由+x轴上某一位置无初速度释放.