题目内容
14. 如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )| A. | 当m到达最高点时,m的加速度为$(1+\frac{M}{m})g$ | |
| B. | 当m到达最高点时,M的加速度为g | |
| C. | 当m速度最大时,弹簧的形变最为$\frac{Mg}{k}$ | |
| D. | 当m速度最大时,M对地面的压力为Mg |
分析 当m到达最高点时,M恰好对地面无压力.此时M受到的弹簧的拉力等于M的重力,在对m受力分析,根据牛顿第二定律求得加速度,当m速度最大时,m的加速度为0,即可判断
解答 解:A、当弹簧处于伸长至最长状态时,M刚好对地面没有压力,可知弹簧对M的拉力为Mg,所以弹簧对m的作用力也是Mg,所以m的加速度为:
${a}_{m}=\frac{mg+Mg}{m}=(1+\frac{M}{m})g$.故A正确;
B、当弹簧处于伸长至最长状态时,M刚好对地面没有压力,可知弹簧对M的拉力为Mg,M受到的合力为零,加速度为零,故B错误;
C、由题可知开始时弹簧对m的弹力大于m的重力,m向上做加速运动,当弹簧的弹力小于m的重力时,m做减速运动,所以弹簧中弹力等于Mg时此时M有最大速度,由胡克定律得:mg=kx,得:x=$\frac{mg}{k}$.故C错误;
D、对M受力分析FN+kx-Mg=0,解得FN=Mg-mg.故D错误.
故选:A
点评 本题主要考查了弹簧的弹力对Mm的运动分析,关键是抓住当,当m处于最高点时,M刚好要离开地面时;弹簧的弹力等于M的重力时.难度适中

练习册系列答案
相关题目
5. 如图所示,水平铜盘半径为r,置于磁感强度为B,方向竖直向下的匀强磁场中,铜盘绕过中心轴以角速度ω做匀速圆周运动,铜盘的电阻不计,铜盘的中心及边缘处分别用滑片与一理想变压器的原线圈相连,理想变压器原副线圈匝数比为n,变压器的副线圈与一电阻为R的负载和电容为C的平行板电容器相连,则( )
如图所示,水平铜盘半径为r,置于磁感强度为B,方向竖直向下的匀强磁场中,铜盘绕过中心轴以角速度ω做匀速圆周运动,铜盘的电阻不计,铜盘的中心及边缘处分别用滑片与一理想变压器的原线圈相连,理想变压器原副线圈匝数比为n,变压器的副线圈与一电阻为R的负载和电容为C的平行板电容器相连,则( )
 如图所示,水平铜盘半径为r,置于磁感强度为B,方向竖直向下的匀强磁场中,铜盘绕过中心轴以角速度ω做匀速圆周运动,铜盘的电阻不计,铜盘的中心及边缘处分别用滑片与一理想变压器的原线圈相连,理想变压器原副线圈匝数比为n,变压器的副线圈与一电阻为R的负载和电容为C的平行板电容器相连,则( )
如图所示,水平铜盘半径为r,置于磁感强度为B,方向竖直向下的匀强磁场中,铜盘绕过中心轴以角速度ω做匀速圆周运动,铜盘的电阻不计,铜盘的中心及边缘处分别用滑片与一理想变压器的原线圈相连,理想变压器原副线圈匝数比为n,变压器的副线圈与一电阻为R的负载和电容为C的平行板电容器相连,则( )| A. | 变压器副线圈两端的电压为$\frac{{B{r^2}ω}}{2n}$ | |
| B. | 通过负载R的电流为$\frac{{B{r^2}ω}}{2nR}$ | |
| C. | 电容器带电荷量为$\frac{{CB{r^2}ω}}{2n}$ | |
| D. | 飞入平行板电容器中的电子沿直线运动(电子重力不计) |
3.如图甲所示的电路中,理想变压器原、副线圈匝数比为5:1,电压表和电流表均为理想电表,R0=10Ω,R1=20Ω,R为滑动变阻器,当在原线圈两端接入如图乙所示的电压时,下列说法中正确的是( )


| A. | 原线圈两端输入电压的有效值为100V | |
| B. | 当滑动变阻器R的滑片向下滑动时,电流表的示数将变大 | |
| C. | 当滑动变阻器连入电路的阻值等于20Ω时,电流表的示数为0.2A | |
| D. | 无论滑动变阻器的滑片如何滑动,原线圈的输入功率均不发生变化 |
4. 一可视为质点的滑块在一个二维空间运动,取互相垂直的两个方向建立xy坐标系,经测量可知x方向的速度-时间图象和y方向的位移-时间图象如图所示,则下列说法正确的是( )
一可视为质点的滑块在一个二维空间运动,取互相垂直的两个方向建立xy坐标系,经测量可知x方向的速度-时间图象和y方向的位移-时间图象如图所示,则下列说法正确的是( )
 一可视为质点的滑块在一个二维空间运动,取互相垂直的两个方向建立xy坐标系,经测量可知x方向的速度-时间图象和y方向的位移-时间图象如图所示,则下列说法正确的是( )
一可视为质点的滑块在一个二维空间运动,取互相垂直的两个方向建立xy坐标系,经测量可知x方向的速度-时间图象和y方向的位移-时间图象如图所示,则下列说法正确的是( )| A. | 前2s内质点的加速度恒定 | |
| B. | 质点具有沿x轴方向的初速度,大小为8m/s | |
| C. | 2s末质点的速度大小为0 | |
| D. | 前2s内质点的轨迹为直线 |
 某实验兴趣小组要测量一个用电器L的额定功率(额定电压为10V、额定功率在12W~15W之间),测量电路采用限流式接法,部分导线已经接好(如图所示).实验室有下列器材可供选用:
某实验兴趣小组要测量一个用电器L的额定功率(额定电压为10V、额定功率在12W~15W之间),测量电路采用限流式接法,部分导线已经接好(如图所示).实验室有下列器材可供选用: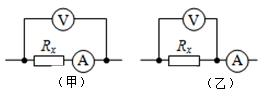 甲、乙两学习小组在用伏安法测电阻大小的实验中,测量电路分别使用了图(甲)、(乙)两种电流表的连接方式.已知:待测电阻Rx约为100Ω,电压表
甲、乙两学习小组在用伏安法测电阻大小的实验中,测量电路分别使用了图(甲)、(乙)两种电流表的连接方式.已知:待测电阻Rx约为100Ω,电压表 的内阻约为3kΩ,电流表
的内阻约为3kΩ,电流表 的内阻约为2Ω.若将图(甲)和图(乙)中电路测得的电阻值分别极为Rx1和Rx2,则Rx1(填“Rx1”或“Rx2”)更接近待测电阻的真实值,且测量值Rx1大于(填“大于”、“等于”或“小于”)真实值,测量值Rx2小于(填“大于”、“等于”或“小于”)真实值.
的内阻约为2Ω.若将图(甲)和图(乙)中电路测得的电阻值分别极为Rx1和Rx2,则Rx1(填“Rx1”或“Rx2”)更接近待测电阻的真实值,且测量值Rx1大于(填“大于”、“等于”或“小于”)真实值,测量值Rx2小于(填“大于”、“等于”或“小于”)真实值. 如图所示,一质量为m的小物块放在斜面上.在物块上施加一力F,且F=$\frac{1}{2}$mg.已知斜面的倾角θ=30°,小物块与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.
如图所示,一质量为m的小物块放在斜面上.在物块上施加一力F,且F=$\frac{1}{2}$mg.已知斜面的倾角θ=30°,小物块与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$. 在工业化高度发展的今天,传动带已成为物料搬运系统机械化和自动化不可缺少的组成部分;未来传动带设备将向着大型化、扩大使用范围、物料自动分拣、降低能量消耗、减少污染等方面发展.如图所示,在煤炭运输线上,传送带以速度v=2m/s匀速转动,煤块被静止释放于A点,煤块与传送带间的动摩擦因数μ=0.5.最大静摩擦力等于滑动摩擦力,此后其运动至B点最后到达C点,已知AB间距离为10.4m,BC长度为8m且与水平面间夹角θ=37°,重力加速度大小g=10m/s2,sin37°=0.6,cos37°=0.8,求:
在工业化高度发展的今天,传动带已成为物料搬运系统机械化和自动化不可缺少的组成部分;未来传动带设备将向着大型化、扩大使用范围、物料自动分拣、降低能量消耗、减少污染等方面发展.如图所示,在煤炭运输线上,传送带以速度v=2m/s匀速转动,煤块被静止释放于A点,煤块与传送带间的动摩擦因数μ=0.5.最大静摩擦力等于滑动摩擦力,此后其运动至B点最后到达C点,已知AB间距离为10.4m,BC长度为8m且与水平面间夹角θ=37°,重力加速度大小g=10m/s2,sin37°=0.6,cos37°=0.8,求: 如图所示,一劲度系数为k的轻质弹簧,上端固定,下端连一质量为m的物块A,A放在质量也为m的托盘B上,以N表示B对A的作用力,x表示弹簧的伸长量.初始时,在竖直向上的力F作用下系统静止,且弹簧处于自然状态(x=0).现改变力F的大小,使B以$\frac{g}{2}$的加速度匀加速向下运动(g为重力加速度,空气阻力不计),此过程中N或F随x变化的图象正确的是( )
如图所示,一劲度系数为k的轻质弹簧,上端固定,下端连一质量为m的物块A,A放在质量也为m的托盘B上,以N表示B对A的作用力,x表示弹簧的伸长量.初始时,在竖直向上的力F作用下系统静止,且弹簧处于自然状态(x=0).现改变力F的大小,使B以$\frac{g}{2}$的加速度匀加速向下运动(g为重力加速度,空气阻力不计),此过程中N或F随x变化的图象正确的是( )


