题目内容
9. 如图所示,一质量为m的小物块放在斜面上.在物块上施加一力F,且F=$\frac{1}{2}$mg.已知斜面的倾角θ=30°,小物块与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.
如图所示,一质量为m的小物块放在斜面上.在物块上施加一力F,且F=$\frac{1}{2}$mg.已知斜面的倾角θ=30°,小物块与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.(1)若力F的方向平行于斜面向下,求小物块的加速度大小;
(2)当力F与斜面的夹角多大时,小物块的加速度最大?并求出最大加速度.
分析 (1)以物体为研究对象进行受力分析,根据牛顿第二定律列方程求解;
(2)画出小物块的受力图,根据牛顿第二定律和摩擦力的计算公式得到加速度的表达式,根据数学知识求解最大值.
解答 解:(1)以物体为研究对象进行受力分析如图所示:
由题意可得:F+mgsinθ-μmgciosθ=ma,
代入数据解得:a=$\frac{1}{2}g$;
(2)小物块的受力如图,设力F与斜面的夹角为α,
根据题意得:Fcosα+mgsinθ-f=ma,
而f=μ(mgcosθ-Fsinα),
联立解得:a=$\frac{1}{2}gcosα+\frac{\sqrt{3}}{6}gsinα=\frac{\sqrt{3}}{3}gsin(60°+α)$,
当α+60°=90° 时,a有最大值,
解得α=30°,am=$\frac{\sqrt{3}}{3}g$.
答:(1)若力F的方向平行于斜面向下,小物块的加速度大小为$\frac{1}{2}g$;
(2)当力F与斜面的夹角为30°时,小物块的加速度最大,最大加速度为$\frac{\sqrt{3}}{3}g$.
点评 本题主要是考查了牛顿第二定律的知识;利用牛顿第二定律答题时的一般步骤是:确定研究对象、进行受力分析、进行正交分解、在坐标轴上利用牛顿第二定律建立方程进行解答.

练习册系列答案
相关题目
20. 嵩山异常险峻,为方便游客,景区设置了索道,如图所示倾斜索道与水平面间的夹角为30°,当载人车厢沿钢索匀加速向上运动时,车厢内站立的人对厢底的压力为其体重的2倍,车厢对人的摩擦力大小为其体重的( )
嵩山异常险峻,为方便游客,景区设置了索道,如图所示倾斜索道与水平面间的夹角为30°,当载人车厢沿钢索匀加速向上运动时,车厢内站立的人对厢底的压力为其体重的2倍,车厢对人的摩擦力大小为其体重的( )
 嵩山异常险峻,为方便游客,景区设置了索道,如图所示倾斜索道与水平面间的夹角为30°,当载人车厢沿钢索匀加速向上运动时,车厢内站立的人对厢底的压力为其体重的2倍,车厢对人的摩擦力大小为其体重的( )
嵩山异常险峻,为方便游客,景区设置了索道,如图所示倾斜索道与水平面间的夹角为30°,当载人车厢沿钢索匀加速向上运动时,车厢内站立的人对厢底的压力为其体重的2倍,车厢对人的摩擦力大小为其体重的( )| A. | 2倍 | B. | $\sqrt{3}$倍 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
17.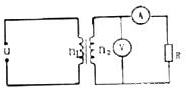 如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
 如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )
如图所示,理想变压器原线圈的输入电压u=1000$\sqrt{2}$sin200πt(V),变压器副线圈与一个定值电阻R=100Ω相连,变压器原、副线圈的匝数n1:n2=10:1,电压表和电流表均是理想交流表,下列说法正确的是( )| A. | 输人电压为正弦交变电压,其周期T=O.02s | |
| B. | 电压表的示数为100V,电流表的示数为1OA | |
| C. | 电压表的示数为I00在v,电流表的示数为1O$\sqrt{2}$A | |
| D. | 电阻R消耗的电功率为100W |
4. 如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
 如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )
如图所示,滑轮A可沿倾角60°的足够长轨道下滑,滑轮下用轻绳挂着一个重力为G的物体B,下滑时,物体B相对于A静止,绳与竖直方向夹角为30°,则下滑过程中(不计空气阻力)( )| A. | A、B的加速度为gsin60° | B. | A、B的加速度为gsin30° | ||
| C. | 绳的拉力为Gcos30° | D. | 滑轮A与轨道之间一定有摩擦 |
14. 如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
 如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图所示,质量分别为M和m的两物块与竖直轻弹簧相连,在水平面上处于静止状态,现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )| A. | 当m到达最高点时,m的加速度为$(1+\frac{M}{m})g$ | |
| B. | 当m到达最高点时,M的加速度为g | |
| C. | 当m速度最大时,弹簧的形变最为$\frac{Mg}{k}$ | |
| D. | 当m速度最大时,M对地面的压力为Mg |
1. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,则( )| A. | 小球所带电荷量为$\frac{b+mg}{E}$ | B. | 轻绳的长度为$\frac{a}{b}$ | ||
| C. | 小球在最高点时的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最低点时的最小速度为$\sqrt{\frac{5a}{m}}$ |
18. 如图所示,A、B两物块质量相同,静止叠放在水平地面上,A、B间的动摩擦因数是B与地面间的动摩擦因数的5倍,可认为最大静摩擦力等于滑动摩擦力.若将水平力作用在A上,使A、B刚好发生相对滑动,此时A的加速度为a1;若将水平力作用在B上,也使A、B刚好发生相对滑动,此时B的加速度为a2,则a1与a2的比为( )
如图所示,A、B两物块质量相同,静止叠放在水平地面上,A、B间的动摩擦因数是B与地面间的动摩擦因数的5倍,可认为最大静摩擦力等于滑动摩擦力.若将水平力作用在A上,使A、B刚好发生相对滑动,此时A的加速度为a1;若将水平力作用在B上,也使A、B刚好发生相对滑动,此时B的加速度为a2,则a1与a2的比为( )
 如图所示,A、B两物块质量相同,静止叠放在水平地面上,A、B间的动摩擦因数是B与地面间的动摩擦因数的5倍,可认为最大静摩擦力等于滑动摩擦力.若将水平力作用在A上,使A、B刚好发生相对滑动,此时A的加速度为a1;若将水平力作用在B上,也使A、B刚好发生相对滑动,此时B的加速度为a2,则a1与a2的比为( )
如图所示,A、B两物块质量相同,静止叠放在水平地面上,A、B间的动摩擦因数是B与地面间的动摩擦因数的5倍,可认为最大静摩擦力等于滑动摩擦力.若将水平力作用在A上,使A、B刚好发生相对滑动,此时A的加速度为a1;若将水平力作用在B上,也使A、B刚好发生相对滑动,此时B的加速度为a2,则a1与a2的比为( )| A. | 1:5 | B. | 3:5 | C. | 5:1 | D. | 5:3 |
19. 两木块1、2质量分别为m,M,用劲度系数为K的轻弹簧连在一起,放在水平地面上.如图所示,用外力将木块1压下一段距离静止,释放后1做简谐运动.在1的振动过程中,木块2刚好始终未离开地面,则在木块1振动的过程中( )
两木块1、2质量分别为m,M,用劲度系数为K的轻弹簧连在一起,放在水平地面上.如图所示,用外力将木块1压下一段距离静止,释放后1做简谐运动.在1的振动过程中,木块2刚好始终未离开地面,则在木块1振动的过程中( )
 两木块1、2质量分别为m,M,用劲度系数为K的轻弹簧连在一起,放在水平地面上.如图所示,用外力将木块1压下一段距离静止,释放后1做简谐运动.在1的振动过程中,木块2刚好始终未离开地面,则在木块1振动的过程中( )
两木块1、2质量分别为m,M,用劲度系数为K的轻弹簧连在一起,放在水平地面上.如图所示,用外力将木块1压下一段距离静止,释放后1做简谐运动.在1的振动过程中,木块2刚好始终未离开地面,则在木块1振动的过程中( )| A. | 木块1的最大加速度为g | |
| B. | 木块1的最大加速度为g+$\frac{M}{m}$g | |
| C. | 木块2对地面的最大压力为2mg+Mg | |
| D. | 弹性势能的变化量、m动能的变化量、m的重力势能的变化量的代数和保持为零 |
