题目内容
3.一个小球和轻质弹簧组成的系统按x1=5sin(8πt+$\frac{π}{4}$)cm的规律振动.(1)求该振动的周期、频率、振幅和初相;
(2)另一简谐运动的表达式为x2=5sin(8πt+$\frac{5}{4}$π)cm,求它们的相位差.
分析 (1)由振动方程可直接读出该振动的角频率ω、振幅和初相;再求解周期和频率.
(2)另一简谐运动的表达式为x2=5sin(8πt+$\frac{5}{4}$π)cm,读出相位,再求得它们的相位差.
解答 解:(1)根据振动方程x1=5sin(8πt+$\frac{π}{4}$)cm,知该振动的角频率ω=8π rad/s,振幅为5cm,初相是$\frac{π}{4}$.
则周期为 T=$\frac{2π}{ω}$=0.25s,频率 f=$\frac{1}{T}$=4Hz
(2)x1与x2的相位差△φ=(8πt+$\frac{π}{4}$)-(8πt+$\frac{5}{4}$π)=-π
答:
(1)该振动的周期是0.25s、频率是4Hz、振幅是5cm,初相是$\frac{π}{4}$.
(2)x1与x2的相位差是-π.
点评 本题的关键要掌握振动方程的一般表达式x=Asin(ωt+φ),知道式中A是振幅,ω是角频率,φ是初相.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
13.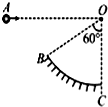 如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )
如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )
 如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )
如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在圆心O的正下方,∠BOC=60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入圆轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动.重力加速度大小为g.则( )| A. | 从B到C,小球克服摩擦力做功为mgR | |
| B. | 从B到C,小球与轨道之间摩擦力逐渐减小 | |
| C. | 在C点,小球对轨道的压力大小等于mg | |
| D. | A、B两点间的距离为$\sqrt{\frac{7}{12}}$R |
8. 甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )
甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )
 甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )
甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )| A. | t=0时甲在乙的前方27m处 | B. | t=0时乙在甲的前方27m处 | ||
| C. | t=6s时,甲的速度大于乙的速度 | D. | t=6s之后两物体不会再相遇 |
15.下列属于矢量的物理量是( )
| A. | 功 | B. | 功率 | C. | 动能 | D. | 速度 |
 如图所示,每个钩码重1.0N,弹簧测力计自身重量、绳子质量和摩擦不计,弹簧伸长了5cm(在弹簧的弹性限度内).该弹簧测力计的示数为1.0 N,该弹簧的劲度系数为20N/m.
如图所示,每个钩码重1.0N,弹簧测力计自身重量、绳子质量和摩擦不计,弹簧伸长了5cm(在弹簧的弹性限度内).该弹簧测力计的示数为1.0 N,该弹簧的劲度系数为20N/m.
