题目内容
3. 如图甲所示,倾角为30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨间距L=1m.一质量m=2kg,阻值r=1Ω的金属棒,在作用于棒中点、沿导轨向上加速运动,棒运动的速度一位移像如图乙所示(b点为位置坐标原点).若金属棒与导轨间动摩擦因数$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属杆从起点b沿导轨向上运动x=1m的过程中( )
如图甲所示,倾角为30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨间距L=1m.一质量m=2kg,阻值r=1Ω的金属棒,在作用于棒中点、沿导轨向上加速运动,棒运动的速度一位移像如图乙所示(b点为位置坐标原点).若金属棒与导轨间动摩擦因数$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属杆从起点b沿导轨向上运动x=1m的过程中( )| A. | 金属棒做匀加速直线运动 | |
| B. | 电阻R产生的焦耳热为0.5J | |
| C. | 通过电阻R的感应电荷量为0.5C | |
| D. | 金属棒与导轨间因摩擦产生的热量为10J |
分析 结合匀变速直线运动的速度位移公式列式分析运动性质;摩擦产生的热量等于克服摩擦力做的功;根据功能关系求解产生的焦耳热;根据电流的平均值求解电量.
解答 解:A、v-x图象是直线,如果是匀加速直线运动,由v2-v02=2ax可知,v-x图象应该是曲线,由图示图象可知,图象是直线,则金属棒做变加速直线运动,故A错误;
B、电路中产生的焦耳热等于克服安培力做的功,为:Q=FA•∑x=$\frac{{B}^{2}{L}^{2}v}{R+r}$∑x,结合v-x图象,其中v•∑x为图象与横轴包围的面积,故v•∑x=1,故Q═$\frac{{B}^{2}{L}^{2}v}{R+r}$∑x=0.5J,由于R=r,故R产生的焦耳热为0.25J,故B错误;
C、通过电阻R的感应电荷量:q=$\overline{I}$t=$\frac{△Φ}{R+r}$=$\frac{BLx}{R+r}$=$\frac{1×1×1}{1+1}$C=0.5C,故C正确;
D、金属棒与导轨间因摩擦产生的热量等于克服摩擦力做的功,为:Q1=μmgcos30°•x=$\frac{\sqrt{3}}{3}$×2×10×$\frac{\sqrt{3}}{2}$×1=10J,故D正确;
故选:CD.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
11. 如图,bc间电阻为R,其他电阻均可忽略,ef是一电阻不计的水平放置的导体棒,质量为m,棒的两端分别与竖直框架保持良好接触,又能沿框架无摩擦下滑,整个装置放在与框架垂直的匀强磁场中,当ef从静止下滑经一段时间后闭合S,则( )
如图,bc间电阻为R,其他电阻均可忽略,ef是一电阻不计的水平放置的导体棒,质量为m,棒的两端分别与竖直框架保持良好接触,又能沿框架无摩擦下滑,整个装置放在与框架垂直的匀强磁场中,当ef从静止下滑经一段时间后闭合S,则( )
 如图,bc间电阻为R,其他电阻均可忽略,ef是一电阻不计的水平放置的导体棒,质量为m,棒的两端分别与竖直框架保持良好接触,又能沿框架无摩擦下滑,整个装置放在与框架垂直的匀强磁场中,当ef从静止下滑经一段时间后闭合S,则( )
如图,bc间电阻为R,其他电阻均可忽略,ef是一电阻不计的水平放置的导体棒,质量为m,棒的两端分别与竖直框架保持良好接触,又能沿框架无摩擦下滑,整个装置放在与框架垂直的匀强磁场中,当ef从静止下滑经一段时间后闭合S,则( )| A. | S闭合后一段时间内ef可能做加速运动 | |
| B. | S闭合后ef可能立即做匀速运动 | |
| C. | ef最终速度随S闭合时刻的不同而不同 | |
| D. | ef的机械能与回路内产生的电能之和一定不变 |
18. 如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )
如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )
 如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )
如图所示,光滑水平面上存在有界匀强磁场,直径与磁场宽度相同的金属圆形线框以一定的初速度斜向匀速通过磁场.在必要的时间段内施加必要的水平拉力保证其匀速运动,则( )| A. | 金属框内感应电流先增大后减小 | B. | 水平拉力方向垂直于磁场边界向右 | ||
| C. | 水平拉力的方向与速度方向相同 | D. | 感应电流的方向先顺时针后逆时针 |
13.2016年2月11日,美国科学家宣布探测到引力波,证实了爱因斯坦100年前的预测,弥补了爱因斯坦广义相对论中最后一块缺失的“拼图”.双星的运动是产生引力波的来源之一,假设宇宙中有一双星系统由a、b两颗星体组成,这两颗星绕它们连线的某一点在万有引力作用下作匀速圆周运动,测得a星的周期为T,a、b两颗星的距离为l、a、b两颗星的轨道半径之差为△r(a星的轨道半径大于b星的),则( )
| A. | b星公转的周期为$\frac{l-△r}{l+△r}$T | B. | a、b两颗星的半径之比为$\frac{l}{l-△r}$ | ||
| C. | a星公转的线速度大小为$\frac{π(l+△r)}{T}$ | D. | a、b两颗星的质量之比为$\frac{l-△r}{l+△r}$ |

 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5m,左端接有阻值R=0.3Ω的电阻,一质量m=0.1kg,电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4T,棒在水平向右的外力作用下,由静止开始做加速运动.已知外力的功率P恒定,P=6.4W,当棒的速度达到最大时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比为Q1:Q2=2:1,导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5m,左端接有阻值R=0.3Ω的电阻,一质量m=0.1kg,电阻r=0.1Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4T,棒在水平向右的外力作用下,由静止开始做加速运动.已知外力的功率P恒定,P=6.4W,当棒的速度达到最大时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比为Q1:Q2=2:1,导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求: 如图所示,足够长的两光滑导轨水平放置,两条导轨相距为d,左端MN用阻值不计的导线相连,金属棒ab可在导轨上滑动,导轨单位长度的电阻为r0,金属棒ab的电阻不计.整个装置处于竖直向下的均匀磁场中,磁场的磁感应强度随时间均匀增加,B=kt,其中k为常数.金属棒ab在水平外力的作用下,以速度v沿导轨向右做匀速运动,t=0时,金属棒ab与MN相距非常近.求:
如图所示,足够长的两光滑导轨水平放置,两条导轨相距为d,左端MN用阻值不计的导线相连,金属棒ab可在导轨上滑动,导轨单位长度的电阻为r0,金属棒ab的电阻不计.整个装置处于竖直向下的均匀磁场中,磁场的磁感应强度随时间均匀增加,B=kt,其中k为常数.金属棒ab在水平外力的作用下,以速度v沿导轨向右做匀速运动,t=0时,金属棒ab与MN相距非常近.求: 如图所示,长L1、宽L2的矩形线圈总电阻为R,处于磁感应强度为B的匀强磁场边缘,线圈与磁感线垂直.将线圈以向右的速度v匀速拉出磁场,则拉力F的大小$\frac{{B}^{2}{L}_{2}^{2}v}{R}$; 拉力的功率P$\frac{{B}^{2}{L}_{2}^{2}{v}^{2}}{R}$;拉力做的功W$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}v}{R}$;.线圈中产生的电热Q$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}v}{R}$.
如图所示,长L1、宽L2的矩形线圈总电阻为R,处于磁感应强度为B的匀强磁场边缘,线圈与磁感线垂直.将线圈以向右的速度v匀速拉出磁场,则拉力F的大小$\frac{{B}^{2}{L}_{2}^{2}v}{R}$; 拉力的功率P$\frac{{B}^{2}{L}_{2}^{2}{v}^{2}}{R}$;拉力做的功W$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}v}{R}$;.线圈中产生的电热Q$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}v}{R}$.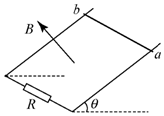 如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求:
如图所示,两平行金属导轨电阻不计,相距L=1m,导轨平面与水平面的夹角θ=37°,导轨的下端连接一个电阻R.匀强磁场的方向垂直于导轨平面向上,磁感应强度为B=0.4T.质量为0.2kg、电阻不计的金属棒垂直放在两导轨上且保持良好接触,金属棒和导轨间的动摩擦因数为μ=0.25.金属棒沿导轨由静止开始下滑,当金属棒下滑的速度达到稳定时,其速度的大小为10m/s.g取10m/s2,已知sin37°=0.6,cos37°=0.8,求: